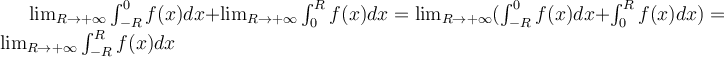FVC-1S: Definición de integral impropia

En el curso de CDIVV se nos dice que cuando uno encuentra una integral impropia, tiene que dividirla de tal forma que cada una tenga un solo problema. Por ejemplo, la integral 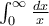$\int_0^{\infty} \frac{dx}{x}$ debería calcularse como 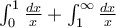$\int_0^{1} \frac{dx}{x} + \int_1^{\infty} \frac{dx}{x}$ . Un ejemplo que recuerdo que se daba para mostrar por qué esto era importante, era el caso de 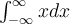$\int_{-\infty}^{\infty} x dx$ , que si se toma de forma correcta diverge, pero si se toma como 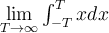$\lim\limits_{T \to \infty} \int_{-T}^T x dx$ converge a 0.

En el video "Un lema de deformación de caminos con aplicación" min 6:30 aparece una integral impropia como el último ejemplo expresada de la forma que lleva al error mencionado.

La pregunta es, bajo qué circunstancias es correcto escribirla así? Es porque ya se demostró previamente que converge?

Re: Definición de integral impropia

de Juliana Xavier - miércoles, 29 de abril de 2020, 10:53

Hola! Gracias por la pregunta. Muy atinada :) Las integrales impropias deben calcularse como vos decís, como se enseña en CDIVV.

La integral impropia converge solamente si convergen ambos sumandos "con un solo problema" como dijiste. Pero cuando ambos sumandos convergen, vale que la suma de los límites es el límite de la suma, y por lo tanto podés "juntar" y calcular el límite de una. Es decir:

$\lim_{R\to +\infty} \int _{-R}^0 f(x)dx + \lim_{R\to +\infty} \int _{0}^R f(x)dx = \lim_{R\to +\infty} ( \int _{-R}^0 f(x)dx + \int _{0}^R f(x)dx ) = \lim_{R\to +\infty} \int _{-R}^R f(x)dx$

Pero para la primer igualdad tenés que saber que ambos sumandos convergen.

Fijate que en este caso la función vale lo mismo en x que en -x , por lo tanto la interal entre -R y 0 vale exactamente lo mismo que entre 0 y R. Por lo tanto una converge si y solo si la otra converge. Y la de 0 a R converge porque estás dividiendo por un x^4.

Osea la respuesta a tu pregunta: La pregunta es, bajo qué circunstancias es correcto escribirla así? Es porque ya se demostró previamente que converge?

Lo que hay que demostrar que converge es CADA SUMANDO, y en ese caso la suma de los límites es el límite de la suma .

Cualquier cosa a las órdenes! Saludos