Hola, no entiendo muy bien de que me sirve saber que todos los números son menores que un k y no he podido pensar en ningún algoritmo de orden n, si me pudieran dar una mano
Hola, yo tambien tengo algunas al respecto de este ejercicio. Adjunto mi resolucion. La idea fue armarme un arreglo auxiliar de tamanio k que contara la cantidad de veces que aparece cada valor en el arreglo A. Esta recorrida es de orden n. Luego, recorria en orden el arreglo auxiliar en orden, copiando tantas veces como aparecia un numero dado en A. O sea si tenia en la casilla que me cuenta la cantidad de 4s, un 3 , copiaba en A (en orden) 3 4s. Creo que la complejidad es O(max{n,k}) pero no se me ocurrio algo mejor.
void sort1_k (int *A, int n, int k) {
// Arreglo que cuenta en la celda h, cuantos valores hay en A que valgan h + 1
// O(1) ????
int *aux = new int[k];
int i, j = 0;
// Inicializar contadores en 0
// O(k)
for (i = 0; i < k; i++)
aux[i] = 0;
// Contar elementos en A clasificados segun valor
// O(n)
for (i = 0; i < n; i++)
aux[A[i] + 1] += 1;
// Copiar en orden valores de A
// O(max{k, n})
for (i = 0; i < k; i++)
while (aux[i] > 0) {
A[j] = i + 1;
j++;
aux[i]--;
}
// O(1) ?????
delete [] aux;
// Orden total : O(max{k, n})
}
Algunas consultas que me quedaron :
1) Las instrucciones delete [] aux y new int[k] son O(1) u O(k)?
2) Es correcto que el orden de este algoritmo es 0(max{k, n}) ?
3) Resuelve bien el problema?
4) Siempre que se tenga O(n + m) tambien se tiene O(max{k, n}) ?
5) Como puedo justificar el calculo del orden? En especial como muestro que el for tiene complejidad el max{n, k},porque si sumo en todos los i de 0 a k - 1 , por construccion el while se va a ejecutar n veces?
Perdón por la demora, había quedado perdida esta pregunta.
1) Asumimos que es O(1). Es una operación que implementa el compilador y no hay razón para suponer que depende del tamaño del bloque de memoria que se pide o devuelve.
2) Sí, y como k es una constante conocida, es O(1) y por lo tanto O(max(k,n)) es O(n).
3) Esa es la idea de como resolverlo.
4) Sí, es la regla del máximo o de la suma (supongo que es m en lugar de k).
5) En el primer for hay exactamente k iteraciones y en el segundo exactamente n iteraciones. En ambos cada iteración es O(1). El tercer for es más interesante y es como argumentás. Vamos a ser más genéricos y suponer que k no es una constante. El tiempo de ejecución es
![\sum_{i=0}^{k-1} (c_1 + \sum_{j=1}^{A[i]} c_2) = c_1 k + c_2 \sum_{i=0}^{k-1} A[i]= c_1k + c_2n](https://eva.fing.edu.uy/filter/tex/pix.php/8a5ec5cce47b03c0a43cf80ed4fbfb59.png "\sum_{i=0}^{k-1} (c_1 + \sum_{j=1}^{A[i]} c_2) = c_1 k + c_2 \sum_{i=0}^{k-1} A[i]= c_1k + c_2n")
donde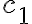 
es el costo de 
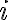y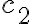 
es el costo de la comparación y cuerpo del while. Ambos, 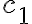y 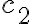son O(1) por lo que el tiempo del tercer for es O(k + n) o lo que es lo mismo O(max(k,n)).
Por lo tanto el tiempo de ejecución es O(k) + O(n) + O(max(k,n)) = O(max(k,n)) por regla del máximo.