Teórico de Deducción Natural - Lógica Proposicional

Hola.

Voy con la idea intuitiva.

Supongamos que nosotros tenemos la fórmula:

@#\alpha \lor \beta#@

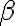Sabemos que la fórmula se cumple¹.... sin embargo no sabemos si se cumple porque $\alpha$ se cumple o porque $\beta$ se cumple o porque las dos se cumplen a la vez.

Entonces si sabemos que 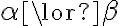$\alpha \lor \beta$ es cierto, qué podemos afirmar que también es cierto en estas condiciones?

Sólo aquellas fórmulas 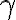$\gamma$ que se pueden derivar de cada parte independientemente. Esas son las fórmulas que se van a cumplir sin importarnos "por culpa de quien" se cumpelen....

Es realmente un análisis de casos: sólo puedo derivar del or, las fórmulas que se pueden derivar de los dos casos a la vez. Las que se derivan de uno pero no se sabe qué pasa en el otro caso, no sirven.

Quedó más claro?

Saludos FDO.

¹ Por "$\alpha$ se cumple" o "$\alpha$ es cierto" son dos formas en las explicaciones del teórico de expresar lo mismo: el hecho que un fórmula nos aparece en la derivación como algo que sabemos que es cierto. Esto puede ser que ya lo sabíamos (por hipótesis) o tenemos una derivación que tiene $\alpha$ como conclusión.