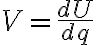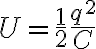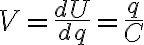Buenas,
Tengo la siguiente duda, definimos que U/q=V la primera vez que tratamos voltaje en el curso. Luego vimos que en un condensador U=q^2/2C. Por ese lado tenemos que en un condensador V=U/q=q/2C. Lo cual esta mal ya que vimos que V=q/C. Porque es que esta mal?
Buenas! Me sumo a la duda planteando una posible respuesta para Martin, ya que no estoy seguro de si es lo correcto. Creo, que en realidad el potencial eléctrico se define como la derivada de la energía potencial con respecto a la carga, esto es 
. Tenemos que en un condensador 
entonces 
que es lo que tenemos para un condensador.
Tu razonamiento es correcto.
Hola Martín,
esta pregunta surgió en una de las clases del consulta x Zoom.
La expresión U = q V define la energía potencial de una carga q en un punto del espacio donde el potencial es V.
La expresión U=q^2/(2C) puede entenderse como la energía almacenada por el capacitor. Interpretamos esta energía, cómo hace Nicolás en la Clase 10 de OpenFing (alrededor del min 60), cómo el trabajo total necesario para crear la distribución de cargas del condensador. La energía necesaria para crear esa configuración de cargas debe es finalmente almacenada en el campo eléctrico del condensador. Podés también consultar la sección 31-4 del H-R.
Lo interesante es que en el condensador, puedes pensar que comienzas con carga q' (y diferencia de potencial V') y traes una carga dq' a cada placa. Ese cambio en la energía potencial es dU = dq'*V'= q'/C dq'. Integrando dq' desde 0 a la carga final Q, obtienes la energía total en el condensador.
En este caso debes considerar que al cargar el capacitor su carga cambia (tomado en cuenta en la integral), por lo que el voltaje cambia también.
Espero ayude. Cualquier cosa a las órdenes.
Buenas, entiendo que la carga asi como el potencial estan variando, es por eso que buscamos encontrar V(t). Pero no veo por qué hace falta meterse con diferenciales. Yo tengo U(q)=q^2/2C es la energía potencial eléctrica almacenada en un condensador. Luego tengo q(t)= (fem).C(1-e^-(t/rc)) es q(t) en la carga de un condensador. ¿Por qué no puedo tener una U(q(t))? Puedo seguir respetando que la carga y el voltaje varían poniendo en la ecuacion de U que q depende del tiempo, llegando a que V depende del tiempo.
Hola Lucas,
creo que estás confundiendo la dependencia de las funciones.
Está bien lo que decís, tenés una U(q) para cada tiempo. Esa q de la que depende la energía es la carga del condensador en cierto instante (no tiene porqué ser la carga máxima).
Aún así, para calcular la expresión de U en función de q, no podés evitar meterte con diferenciales, ya que estás hablando de una distribución de cargas.
Para un tiempo arbitrario t*, en que la carga es q*=q(t*), la energía potencial almacenada en el condensador es el trabajo necesario para cargarlo. Algo así como traer diferenciales de carga hasta llegar a q* (y eso es equivalente a integrar).
¿Se entiende?