Cuando se pide hallar un par de funciones "diferenciables en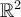 
", se refiere a funciones 
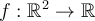? Si se refiere a campos sobre 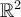, qué producto deberíamos considerar?
Video challenge sobre consecuencias del teorema de los 0's
Número de respuestas: 10
En respuesta a Gabriel Emmanuel Mello Muñoz
Re: Video challenge sobre consecuencias del teorema de los 0's
Se refiere a funciones de R2 a R2, ya que al plano complejo lo podes ver como R2. Ademas imagino q sería un producto escalar, pq el producto entre dos complejos es como una especie de producto escalar o parecido
En respuesta a Gaston Alvarez Dorado
Re: Video challenge sobre consecuencias del teorema de los 0's
De hecho el producto escalar no se parece para nada al producto de complejos. Primero porque si vemos a C como un e.v. sobre R, el producto escalar es un funcional lineal mientras que el producto de complejos es una transformación de C^2 en C (o un operador sobre C si fijamos una de las entradas), y segundo porque el producto escalar cambia radicalmente variando el ángulo entre los vectores, mientras que el módulo del producto de complejos es invariante bajo rotaciones de los argumentos.
En respuesta a Gabriel Emmanuel Mello Muñoz
Re: Video challenge sobre consecuencias del teorema de los 0's
de Juliana Xavier -
Hola! Funciones diferenciables de R^2 en R^2, para hacer la analogía con las funciones de C en C.
En respuesta a Juliana Xavier
Re: Video challenge sobre consecuencias del teorema de los 0's
Y el producto?
En respuesta a Gabriel Emmanuel Mello Muñoz
Re: Video challenge sobre consecuencias del teorema de los 0's
de Juliana Xavier -
No entiendo la pregunta sobre el producto. Por favor desarrolle.
En respuesta a Juliana Xavier
Re: Video challenge sobre consecuencias del teorema de los 0's
En el video se demuestra que si f y g son holomorfas y su producto (producto de números complejos sobre todo el dominio) es la función nula, entonces alguna de las funciones es la función nula. Cuando hablamos de campos sobre R2, de qué forma los multiplicamos para buscar el contraejemplo? Producto escalar, vectorial, entrada a entrada?
En respuesta a Gabriel Emmanuel Mello Muñoz
Re: Video challenge sobre consecuencias del teorema de los 0's
El producto vectorial te da como resultado un vector perpendicular a los otros dos. Te salís del plano
En respuesta a Gaston Alvarez Dorado
Re: Video challenge sobre consecuencias del teorema de los 0's
de Juliana Xavier -
Y con el producto escalar obtenés un real :)
Igual la pregunta es válida en todos los casos. Pregúntenselo en todos los casos!
En respuesta a Gabriel Emmanuel Mello Muñoz
Re: Video challenge sobre consecuencias del teorema de los 0's
de Juliana Xavier -
Ah, como números complejos! Osea f y g de R2 en R2 que cumplan la misma propiedad que las funciones del video (f(z)g(z) =0 para todo z de R2, donde el producto es como números complejos), que sean diferenciables en R2, pero que ni f ni g sean la función idénticamente nula.
Si se te ocurre el ejemplo multiplicando entrada a entrada ponelo también.
Gracias por la pregunta, no estaba claro.
Saludos
En respuesta a Juliana Xavier
Re: Video challenge sobre consecuencias del teorema de los 0's
Clarísimo, gracias!