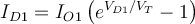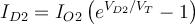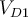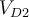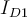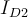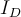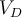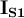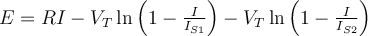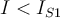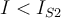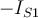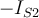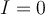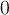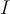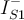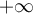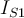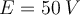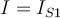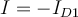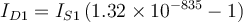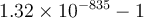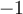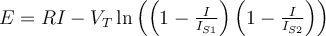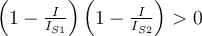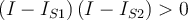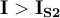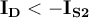Hola Jorge,
Un par de comentarios
1) El error está en que en la ecuación del diodo (Vt*log(Isat/(I+Isat))) ese I, que sería la iD de la ec. del diodo en realidad es -I ya que el I en la malla (RI+V_d1+V_d2=50) es la corriente inversa por el diodo (es decir -iD).
2) El procedimiento que describió Nicolás es el procedimiento correcto para determinar la solución exacta al problema. No obstante esto hay otra manera, más cualitativa e intuitiva, de analizarlo que es la siguiente. Es mirarlo gráficamente teniendo en cuenta la forma que tiene la característica inversa del diodo.
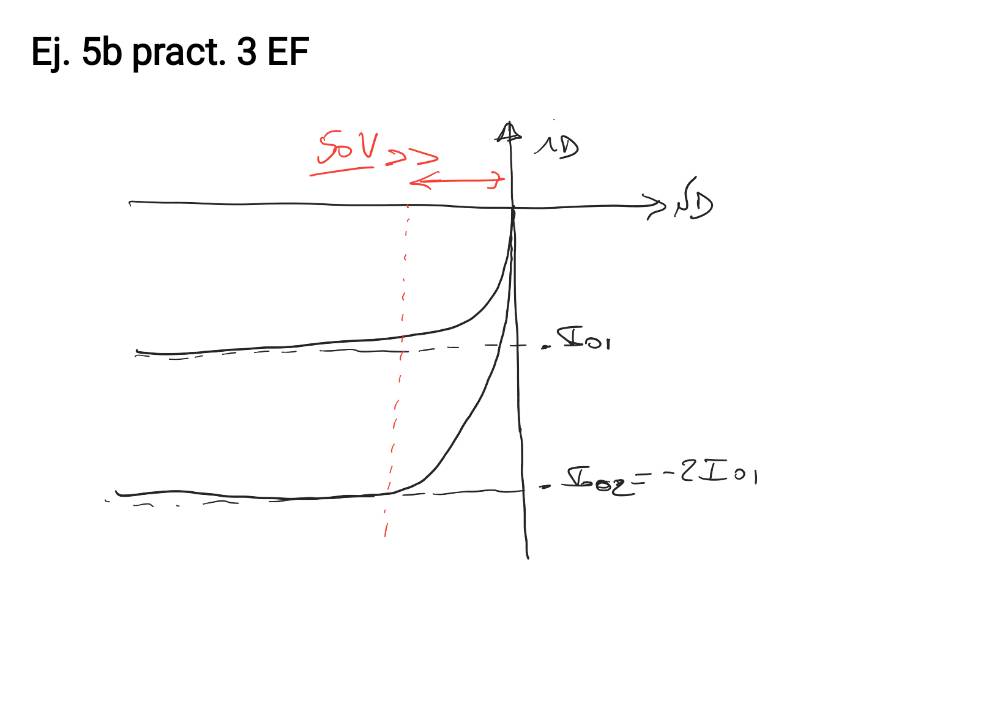
Entonces si graficamos las características inversas de los dos diodos en cuestión tendríamos lo que se muestra en la figura adjunta.
Si observas ahi que ambas curvas tienden a la asíntota para tensiones mucho menores a 50V (es decir que para VD << 50V ocurre que exp(-VD/VT) << 1) y recordando que se trata en definitiva de encontrar dos puntos sobre esas curvas que cumplan que: a) la suma de los voltajes sea cerca de 50V (porque la corriente sabemos que no puede ser muy grande y por tanto tampoco la caida en la R) y b) que la corriente es la misma en ambos diodos, de b) se deduce que la corriente no puede ser mayor a IO1 y de a) y de lo antes indicado (que llegan a la asintota para tensiones pequeñas) se puede ver que la corriente tiene que ser prácticamente IO1. De ahi se ve que el diodo 1 soporta casi toda la tensión aplicada, por lo que no es una buena estrategia usar diodos en inverso en serie.
Otro atajo para llegar a la solución es, sabiendo que la corriente no va poder ser más grande que la IO menor de las dos, ver que la caida en la R va a ser despreciable y esto ya simplifica un poco la parte numérica.
No se si esta explicación a distancia se entendió. Sino, en todo caso lo ver interactivamente en alguna clase de consulta.
Saludos,
Fernando