Un producto interno es lineal en ambas componentes? Podría explicarme eso ?
Buenas.
La afirmación a la que hacés referencia es Falsa.
Por las propiedades 1 y 2 de la definición de Producto Interno, podés ver que un PI siempre es lineal en la primer coordenada.
Pero no siempre es lineal en la segunda coordenada. Tratá de convencerte de esto último.
Recordá que, para que el PI sea lineal en la segunda coordenada, debería cumplirse: 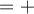 y
y  , para todo
, para todo 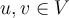 y
y 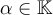 .
.
Matías.
y en qué caso no se cumple eso? Con los imaginarios?
Deberías encontrar un contraejemplo para probar que falla alguna de las dos propiedades que describió Matías.
Puedes probar como ejercicio que la primera propiedad (que se denomina aditividad) sí se cumple, la propiedad que en realidad falla es la segunda (que se denomina homogeneidad).
Para ello, debes encontrar un espacio vectorial V, un producto interno en él, un par de vectores u y v y un α en K que verifiquen
<u, αv>≠α<u,v>.
Saludos,
Florencia.