Me surgió una duda sobre la ecuación para c<0: 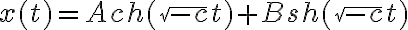
¿Ese -c dentro de las raíces, se debe a que considera el valor negativo del c dado (que en este caso quedaría positivo dado que estamos trabajando con c<0), o a que considera el valor del c dado (o sea, trabajamos con complejos)?

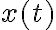
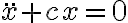

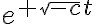
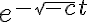
![\sqrt[]{-c} \sqrt[]{-c}](https://eva.fing.edu.uy/filter/tex/pix.php/61e8681e9efe780ea98a4d1fa9e4b2d4.gif)
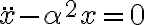
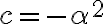
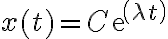
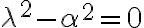
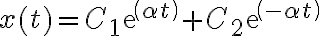
![\alpha = \sqrt[]{-c} \alpha = \sqrt[]{-c}](https://eva.fing.edu.uy/filter/tex/pix.php/2fd5b9ec32f283f1ccb35a85737c1c3f.gif)