Hola,
Luego de resolver este ejercicio integrando de dos maneras diferentes como dice la letra me surge la duda de si hay alguna manera de obtener la solución de la ecuación diferencial original es decir y(t)
Gracias
Para hallar la ley horaria y(t) habría que hallar la dependencia de la velocidad v con el tiempo, o sea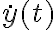 
e integrarla en el tiempo. O sea, invertir la relación que se halla en la parte a i, t(v), para una velocidad 
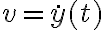genérica e integrar en el tiempo. Creo que involucraría una integral de una tangente. Se puede hacer, pero no se pide.
Ya entiendo, gracias por la respuesta!
Olvidé decir que en este sistema la ley horaria hay que hallarla en dos pasos. Porque hay una ecuación para el movimiento ascendente y otra para el movimiento descendente. Porque cambia la ecuación de movimiento, ya que la fuerza siempre se opone a la velocidad (cambia el módulo de la velocidad). Lo que decía de la tangente es para el movimiento ascendente. Para el movimiento descendente habría que ver si la ecuación diferencial se puede resolver analíticamente.