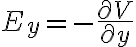Foro de consultas

Hola Lucas, mirá, no se en que formato estas mandando la foto, pero no llega.

De todas formas y para que no pierdas más tiempo te contesto por donde va el ejercicio.

Parte A) Te pide el potencial en P:

Tu diferencial de voltaje es 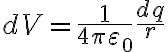$dV=\frac{1}{4\pi\varepsilon_0}\frac{dq}{r}$ siendo $dq=kxdx$ y $r=\sqrt{x^2+y^2}$

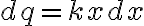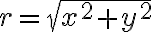
Y este diferencial es el que integras para hallar el voltaje. Por el texto que mandaste, donde hablas de un ángulo en función de la distancia, dedusco que trataste de hallar una componente como se hace en los casos en que se quiere hallar el campo eléctrico.

En esos casos está bien porque a veces una componente del campo eléctrico se anula por simetría y hay que integrar solo considerando la componente en la dirección resultante. Eso es porque el campo  eléctrico es un vector y tiene componentes en varias direcciones.

En el caso del potencial no, porque el potencial es escalar entonces no hay que descartar componentes. Solo depende de la distancia entrer el punto y el diferencial de carga. Por eso el potencial se halla integrando el diferencial de arriba de la siguiente forma:

$V=\frac{k}{4\pi\varepsilon_0}\int_0^L\frac{xdx}{\sqrt{x^2+y^2}}$

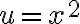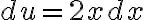cambio de variable $u=x^2$ y $du=2xdx$ hay que hacer aparecer un 2 multiplicando y dividiendo

Entonces:

$V=\frac{k}{8\pi\varepsilon_0}\int_0^{L^2}\frac{du}{\sqrt{y^2+u}}=\frac{k}{4\pi\varepsilon_0}\sqrt{y^2+u}|^{L^2}_0=\frac{k}{4\pi\varepsilon_0}\left[\sqrt{y^2+L^2}-y\right]$

De ahí sale la parte a.

Para la parte B debes tomar la derivada parcial del potencial  para hallar en campo eléctrico:

$E_y=-\frac{\partial V}{\partial y}$

Espero te responda.

Saludos, Enzo.