Buenas!
No estaría entendiendo que me pide el eje 6, o sea entiendo que me pide el factorial con recursivo de cola, pero la especificacion dice que devuelve
el fact(n)*acum?
La versión recursiva vista de factorial no es con recursión de cola. La idea es que la implementación de factorial invoque esta nueva función, que debe ser recursiva y con recursión de cola.
Tenemos que implementar factAcum(n, acum) para que el resultado devuelto sea el factorial de n * acum.
Digamos que la función que devuelve el factorial de n se llama miFactorial. Su implementación sería
uint miFactorial (uint n) {
return factAcum(n, ?)
}
¿Cuál debe ser el valor asignado en esa invocación al parámetro acum, para que el valor devuelto por factAcum (teniendo en cuenta la especificación de esta función) sea al factorial de n?
¿Esto aclara el objetivo de factAcum? Después, claro, falta resolverla.
viendo esta explicación que da, no me termina de quedar claro que rol tiene la variable acum en la función ni que valor estaría almacenando en ella
acum es un parámetro en el que se va acumulando el resultado en las sucesivas llamadas recursivas.
Veamos la primera de las preguntas que habían quedado. El resultado de miFactorial(n) debe ser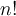 
y se obtiene mediante el llamado a factAcum que si cumple lo que se plantea debe devolver 
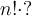.. Entonces tenemos
de donde sabemos que '?' es 1.
Ahora pensemos como resolver factAcum. Tenemos que encontrar algún o algunos casos en que podamos resolver sin llamadas recursivas, o sea del cual conocemos el factorial de n. Podemos tomar n = 0,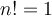 
.
Para un n genérico, mayor que cero, para el que queremos calcular factAcum(n, acum) podemos tomar factAcum(n-1,x). como un caso más cercano al caso base y asumir que sabemos resolverlo. Pero ¿qué valor de x, que podamos calcular en función de n y de acum, nos sirve para que el resultado de factAcum(n-1,x) nos ayude a calcular el de factAcum(n, acum)?
Por ejemplo ¿podremos lograr que se cumpla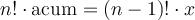 
? Si es así, ¿cuánto tiene que valer x, que sería el segundo parámetro en la llamada recursiva para calcular factAcum(n, acum)?
Buenas estuve leyendo los mensajes y la verdad que no veo lo que sucede. Los mensajes parecen claros pero no logro captar lo que hay que hacer, o sea la función que pide el ejercicio es una que va a ser implementada dentro de otra? Si es así a que se refiere con recursión de cola, se que esta en el teórico , lo leí y no lo termine de entender. Tampoco entiendo porque el factorial de teórico no es recursión de cola.
No dije nada.