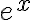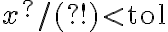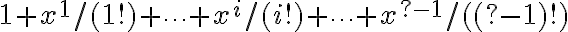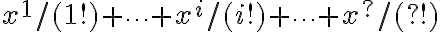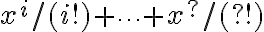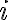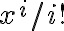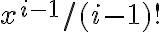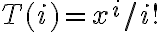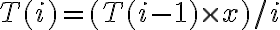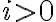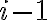Buenas tardes!
No se como hacer que la función termine en el ejercicio número 11; se que tengo que hacer variar la cantidad porque es el único parámetro que puedo modificar, pero a su vez cantidad va aumentando y no se como hacer para que la función termine. Espero que puedan darme una idea como para parar la recursividad.
Saludos.
No, cantidad es uno de los valores que tenés que devolver. No te sirve para determinar si estás en el caso base.
Vamos a empezar por algo más sencillo. Supongamos que la función no nos pide devolver cantidad, sino solo la aproximación de 
.
¿Qué tiene que pasar para dejar de calcular? Si te resulta más fácil, y para entender el problema, pensalo con un enfoque iterativo y después vemos como lo haríamos con uno recursivo.
Gracias por la respuesta.
Igual creo que no se entendió bien mi pregunta. Yo sé que para hacer el caso base, lo que tiene que suceder es que (tol<ultimo término). Pero lo que no me queda claro, es en el llamado de la función recursiva. Si yo pongo exp(x,tol,cantidad), el único parámetro que podría modificar para que la función alguna vez termine es cantidad, pero no sabría como hacerlo. Además, tampoco entiendo bien cuál sería el caso base.
Perdón por las molestias y gracias.
Claro, pero si el problema fuera más fácil y no pidiera que se devuelva la cantidad seguramente no incluirías cantidad en la especificación de la función. O sea, que no es eso lo que hay que modificar.
Debe quedar claro que este ejercicio es difícil. Por eso primero vamos a olvidarnos de calcular la cantidad. Después lo agregamos.
Vamos a tener que diseñar otra función, a la cuál la función que ya tenemos llamaría, como habrás visto en otros ejercicios. Esa nueva función va a generalizar el problema.
Lo que queremos calcular es
donde pongo '?' porque no sabemos cuál es. Lo que sabemos es que es el primero que cumple 
.
Tenemos que encontrar cuál es la estructura recursiva, cómo se puede obtener algo "más chico" a lo que se le pueda aplicar el mismo problema. Ese problema no tiene por qué ser el original. Casi siempre lo es, pero a veces, como ahora, el problema a resolver es una generalización del original.
Vamos a ver cómo podríamos "achicar" la expresión anterior.
Lo que uno primero piensa es
Pero, ¿cómo sería el mismo problema?, ¿cómo hacer aparecer 
en esta expresión?
La otra es
en donde '?' es exactamente el mismo de arriba y está relacionado con .
Entonces en la generalización nuestro nuevo problema es calcular
(para resolver el problema original hay que llamar a la función que invoca éste con 0 como parámetro en lugar de 
).
¿Se va entendiendo hasta acá?
¿Qué parámetro habría que agregarle a la función original para la nueva función? ¿Cuál sería el caso base y cómo se detecta?
Todavía falta, la seguimos.
Hola. No sé si con el mensaje anterior alcanzó. Como supongo que el atención va a pasar a los siguientes temas del curso vamos a tratar de redondear este ejercicio.
Creamos una función que generaliza la anterior. Vamos a llamarla expRec. Obviamente x y tol siguen siendo parámetros a los que agregamos i, que identifica el término. Evaluamos el término i-ésimo,llamémosle evalTermino. Con esa evaluación sabemos si estamos en el caso base o no.
float expRec( x, tol, i)
evalTermino = x^i / i!
si evalTermino > tol
resultado = evalTermino + expRec(x, tol, i + 1)
en otro caso
resultado = evalTermino
return resultado
Y así sería la versión más simple.
Teniendo en cuenta el subhilo que inició Martín se podría hacer más eficiente el cálculo de evalTermino. Para eso ese valor se pasa como parámetro en la llamada recursiva. La evaluación del nuevo término sería evalTermino = evalTermino * x / i.
Finalmente para agregar la cantidad de términos evaluados se agrega el parámetro cantidad pasado por referencia, como en la función original. Esa cantidad se conoce al llegar al caso base, y es igual a 1 + identificador del término, i. O sea que en el caso base se asigna cantidad = 1 + i.
¿Quedan dudas?Si tu pregunta es cómo calcular el factorial de un número grande, es interesante por sí misma y valdría que abras un nuevo hilo, tal vez relacionado con el ejercicio que calcula el factorial.
Si es para resolver este ejercicio vamos a ver que eso no es una dificultad.
Todavía falta lo más importante, que es saber cómo hacer la recursión en este problema. Pero supongamos que lo tenemos resuelto. Una parte de la resolución es calcular cada término 
. Cuando vamos a calcular este término, tal vez en la ejecución del algoritmo ya se haya calculado 
. ¿Podríamos aprovecharlo?
Es interesante ver que estos términos tienen ellos mismos una estructura recursiva. Llamemos 
. Se cumple
para 
O sea que no hace falta calcular el factorial. Y en lugar de hacer 
multiplicaciones para calcular 
, otras 
para calcular el factorial y una división, se soluciona con una multiplicación y una división.
Lo que queda por ver es como se puede aprovechar esto en la solución del ejercicio.