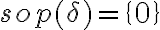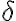hola Francisco,
es una buena pregunta
1) La respuesta es SI.
Uno quiere trabajar con un conjunto de funciones que aseguren que exista siempre que su producto convolución. Existen muchos y la pregunta que hay que hacerse es si las integrales 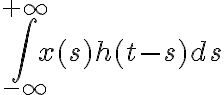 y
y 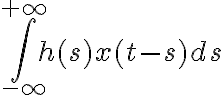 están bien definidas para todo
están bien definidas para todo  .
.
Tu podrías verificar que si las funciones son de soporte acotado, la convolución siempre estará bien definida. También sería el caso de funciones en  por ejemplo.
por ejemplo.
El espacio más cómodo de trabajo es el de las funciones contenidas en 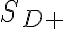 , ya que con este se puede construir un álgebra de convolución (el resultado del producto convolución también sería una función de
, ya que con este se puede construir un álgebra de convolución (el resultado del producto convolución también sería una función de 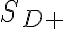 ).
).
2) Tu conclusión respecto al soporte la función es correcta (en ese caso sería el conjunto [0,2]). La discrepancia con lo que tú observas en las notas de sistemas lineales es que ahí se encuentra definido el soporte de un conjunto de funciones "auxiliares" que no son en realidad el objeto de estudio (las distribuciones son el objeto de estudio de ese capítulo).
Para determinar el soporte de las funciones con las que trabajamos aquí la intuición te puede ayudar (donde no es nula y no importa si es o no continua). Una paso más en la formalidad sería decir que el soporte de una función es el menor cerrado fuera del cual la función es nula (que puede ser un poco difícil de interpretar). Veamos un ejemplo:
En el caso del problema que tu planteas, un cerrado que cumpla que fuera de él la función es nula sería, por ejemplo el [-10,10]. Fuera de ese conjunto la función efectivamente es nula, pero no es el menor cerrado. El cerrado más pequeño que cumple la consigna sería el [0,2] arribando al mismo resultado.
Si hay algo que no se entiende, avisen y seguimos por aquí.
Saludos
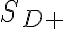 .
La pregunta es, estas propiedades se cumplen si por ejemplo todas las distribuciones
involucradas tienen soporte acotado (que pertenezca o no a
.
La pregunta es, estas propiedades se cumplen si por ejemplo todas las distribuciones
involucradas tienen soporte acotado (que pertenezca o no a 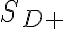 ) ?
) ?
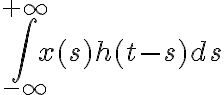
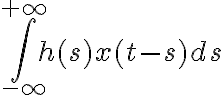


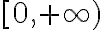
![(-\infty,0] (-\infty,0]](https://eva.fing.edu.uy/filter/tex/pix.php/15a0f0419a82bd06453c59063f91aad0.gif)