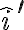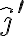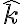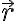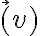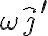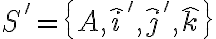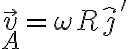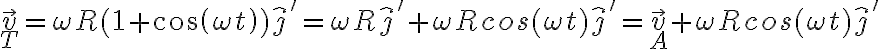MecNew: Ejercicio 11

Buenas, mi consulta es la siguiente: en este problema se tiene que el punto A (centro de la cfa) está rotando con respecto al sistema de coordenadas fijo O,i,j,k, mi sistema móvil 1 fue hecho asi S'=(A,i',j',k), mi consulta es si al derivar la posición de A con respecto a O el eje i' no tendría derivada con respecto al tiempo distinta de 0?

Lo que quiero decir es que intuitivamente dado que el i' se esta moviendo, al hacer su derivada con respecto al tiempo me da Rw.j' , y mi duda es si este término es correcto o no lo es, dado que con ese valor llego a un resultado que no coincide con la resolución.

Saludos

126 palabras

Re: Ejercicio 11

de Leandro Jair Machado Da Silva - lunes, 23 de marzo de 2020, 00:04

Hola Nicolás, me parece que lo que te quedó está bien, capaz la diferencia del resultado final viene por otro lado. El punto A describe un movimiento circular, y la base en coordenadas cilíndricas para ese movimiento sería { $\hat{i}^{\prime}$ , $\hat{j}^{\prime}$ , $\hat{k}$ }. La posición es $\vec{r}$ = R $\hat{i}^{\prime}$ (acordate que lo estamos viendo desde el origen del sistema absoluto, en la base primada) y la velocidad queda $\vec(v)$ = R $\omega \hat{j}^{\prime}$ (podes sacarlo directamente de la expresión general de la velocidad en cilíndricas)

Saludos

94 palabras

Re: Ejercicio 11

de Ariel Fernández - lunes, 23 de marzo de 2020, 09:24

Hola,

gracias de nuevo por responderse entre Uds, es la mejor forma de enriquecer el intercambio.

El término de la velocidad del origen del sistema S' considerado ( $S'=\{A,\hat{i}',\hat{j}',\hat{k}\}$ ) es como bien dicen $\vec{v}_A=\omega R \hat{j}'$ y está incluido en la respuesta del ejercicio ya que es la primera parte de la velocidad de transporte: $\vec{v}_T=\omega R (1+cos(\omega t)) \hat{j}'=\omega R\hat{j}'+\omega Rcos(\omega t)\hat{j}'=\vec{v}_A+\omega Rcos(\omega t)\hat{j}'$ .

Saludos,

Ariel.

97 palabras

Re: Ejercicio 11

de Margaret Wyaux Yewdiukow - lunes, 23 de marzo de 2020, 14:36

Hola,

El primer término de la velocidad de transporte si me quedo según j’, pero el segundo término me queda según ephi.

w x r’= (w según k) x (R según er) = wR según ephi. Me queda igual que la velocidad relativa de M. No sabría cómo relacionarlo con j’.

50 palabras

Re: Ejercicio 11

de Ariel Fernández - lunes, 23 de marzo de 2020, 16:02

Hola,

tanto $\hat{k}$ como $\hat{e}_r$ están contenidos en el plano de la circunferencia, por lo que el producto vectorial entre los dos es perpendicular a ese plano, es decir según $\hat{j}'$ , por lo tanto queda según ese versor el término de la velocidad de transporte que buscás.

Saludos,

Ariel.

53 palabras

Re: Ejercicio 11

de Nicolas Alejandro Scolaro Ribero - lunes, 23 de marzo de 2020, 15:31

Agradezco sus respuestas, mi error fue en el momento de considerar mi w para hallar la velocidad de transporte ya que había puesto que w = (w. k - wj') y razonandolo mejor el w correcto para ver la velocidad de transporte debe ser w = w. k, y ahí si llego al resultado correcto.

Saludos y gracias nuevamente

56 palabras