Buenas!
Acaso debería tomar como si tengo el campo de una esfera uniformemente cargada y restarle el campo que generaría el huequito ese? Va por ahí, lo que tenés que pensar es: cuáles son las distribuciones de carga que hay que sumar para obtener la distribución de la figura? Como dijiste una es la esfera grande con densidad constante 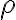 . Qué distribución volumétrica tenés que superponer (sumar) para obtener la de la figura? Luego hay que tomar un punto dentro de la esfera chica y sumar el campo que produce cada distribución allí.
. Qué distribución volumétrica tenés que superponer (sumar) para obtener la de la figura? Luego hay que tomar un punto dentro de la esfera chica y sumar el campo que produce cada distribución allí.
No me cierra la idea de que el campo ahí sea independiente a si está cargado a que si no lo estuviese. No es esto lo que dice la letra que pasa: si no hubiera agujero, el campo sería 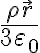 en todo punto, con
en todo punto, con 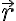 el vector que va del centro de la esfera grande al punto donde estás calculando el campo. En particular, el módulo del campo en este caso es proporcional a la distancia al centro de la esfera grande. Mientras que lo que dice la letra que pasa cuando el agujero no está cargado es que el campo es
el vector que va del centro de la esfera grande al punto donde estás calculando el campo. En particular, el módulo del campo en este caso es proporcional a la distancia al centro de la esfera grande. Mientras que lo que dice la letra que pasa cuando el agujero no está cargado es que el campo es 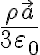 con
con 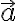 vector que va del centro de la esfera grande al centro de la chica. Esto quiere decir que el campo es igual en todo punto de la esfera chica, sin importar la distancia de ese punto al centro de la esfera grande, ni la distancia de ese punto al centro de la esfera chica.
vector que va del centro de la esfera grande al centro de la chica. Esto quiere decir que el campo es igual en todo punto de la esfera chica, sin importar la distancia de ese punto al centro de la esfera grande, ni la distancia de ese punto al centro de la esfera chica.
Espero que se haya entendido pero si tenés más dudas estamos a las órdenes!
