Hola,
Tus duda toca varios aspectos interesantes.
El usar una lista por comprensión para generar las posibles soluciones es un camino posible y correcto. Tu solución está fuertemente orientada al uso de evaluación perezosa, en el sentido de generar todas las potenciales soluciones y luego quedarse con una de ellas. Gracias al mecanismos de evaluación perezosa (que veremos mas adelante en el curso), en caso que existieran varias soluciones sólo la primera será generada; si no se tuviera un mecanismo así el programa quedaría infinitamente intentando generar soluciones (dado que tu idea es que se intente para cada entero).
En lo que respecta a tu solución, parece razonable intentar con todos los posibles "restos" (los valores "y" entre -4 y 5), pero no así con todos los posibles "z". Analizando matemáticamente el problema uno puede ver que la descomposición que se pide está bastante emparentada con lo que se obtiene haciendo división entera (div) y resto (mod), por lo que no parece razonable intentar con todos los posibles enteros para el caso de "z".
El otro problema es que significa generar la lista (infinita) de enteros. Nos hace meter con algo que vamos a ver mas adelante en el curso. No hay problema con la lista (infinita) de números naturales: nats = [0..]; la podemos ir generando (y recorriendo) a demanda. Podemos escribir como se representaría la lista de enteros negativos: negs = map negate [1..]. Lo que no sería computacionalmente adecuado es pensar que al escribir la lista enteros = nats ++ negs vamos a poder generar todos los enteros. La expersión nats ++ negs tiene el tipo correcto y es aceptada por el compilador. El problema es que la primera lista (nats) es infinita, por lo que habría que esperar hasta la eternidad para poder pasar a la segunda lista (negs). Si uno quisiera (potencialmente) probar soluciones para todos los enteros debería entonces buscar algún mecanismo para generar alternadamente elementos de una lista (nats) y de la otra (negs) de forma de ir avanzando en una y otra de forma pareja. Igualmente, como decía arriba, en este caso particular del ejercicio parece innecesario hacer una solución que intente probar con todos los enteros.
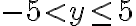 y
y 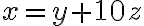 ), colocarlos en una lista que se generara por comprension, y quedarme con el primer y unico
elemento de esta lista. Seria algo asi:
), colocarlos en una lista que se generara por comprension, y quedarme con el primer y unico
elemento de esta lista. Seria algo asi:
