Hola,
no logro comprender del todo el tema de las simetrías y el campo.
Por ejemplo en el ejercicio 4, al elegir un cilindro como superficie gaussiana, se supondría que por simetría el campo eléctrico es radial y constante, no comprendo por que esto es así! lo cual permite resolver la integral para calcular el flujo
si alguien me puede explicar bien lo de las simetrías le agradezco
saludos

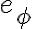
![Adjunto 20200319_191920[1]-min.jpg](https://eva.fing.edu.uy/pluginfile.php/278759/mod_forum/attachment/347676/20200319_191920%5B1%5D-min.jpg?forcedownload=1)