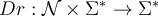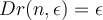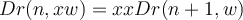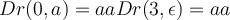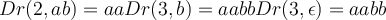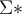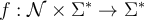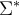Lógica: Recursión en funciones con más de una variable definida de forma inductiva.

Hola, en el teórico mencionamos la siguiente situación:

Si A, B son conjuntos definidos de forma inductiva, sea f; AxB -> C

f(a,b)= ...

f(succ(a),b) = ...f(a,transformado(b))

O sea una función definida inductivamente en cuya llamada recursiva aparecen transformados los dos parametros.

Se afirmo que usar el ERP para AxB era equivalente a usar el ERP para A o para B y me quedo la duda de porque esto es así. Para casos análogos afirmamos que usar el PIP de AxB era equivalente a usar el de A o el de B, pero tampoco entiendo por que esto es así.

Un ejemplo concreto seria la función sacar_izquierda del ejercicio 15 del practico 1, aunque mi pregunta no es puntual sobre este ejercicio.

Re: Recursión en funciones con más de una variable definida de forma inductiva.

de Fernando Carpani - martes, 17 de marzo de 2020, 10:40

Hola Rafael.

En el ERP, se pide que haya una ecuación por regla del conjunto, en cada ecuación se recibe como parámetr una "construcción" del conjunto. La llamada recursiva (a la misma función que estamos definiendo) puede aparecer o no. Pero si lo hace, tiene que hacerlo sólo sobre los elementos del conjunto que se usan en la "construcción" que se recibió como parámetro.

Con respecto a el uso de varios parametros, veamos si con un ejemplo se aclara. Miren la siguiente funcion (DuplicaRaro):

$Dr: \mathcal{N} \times \Sigma^* \to \Sigma^*$

$Dr(n,\epsilon)=\epsilon$

$Dr(n,xw)=xx Dr(n+1,w)$

Fijense lo que hace:

$Dr(0,a)=aa Dr(3,\epsilon) = aa$

$Dr(2,ab)=aa Dr(3,b) = aabb Dr(3,\epsilon)= aabb$

Observer que para aunque se agrande el número !!! Esto es porque la función sigue el esquema de recursión primitiva de

$\Sigma*$ en el segundo parámetro.

Si miramos bien la definición, es una función que aplica la recursión "en la parte de la construcción" que recibe como parámetro. Observar además que el número que se recibe, no se usa. Si se usa, allí podrían aparecer complicaciones (o no :-) ).

Queda más clara la idea?

Saludos

FDO

Re: Recursión en funciones con más de una variable definida de forma inductiva.

de Rafael Agustin Castelli Ottati - miércoles, 18 de marzo de 2020, 11:26

Con el ejemplo se me aclaró bastante la situación. Sin embargo me quedaron un par de dudas:

1) Porqué puedo asegurarme de que eso es una función usando el ERP para Σ∗ , cuando es una función que tiene como dominio a N×Σ∗. No debería usar el ERP para N×Σ∗? Que me permite usar el de Σ∗ nada más?

2) Si bien entiendo intuitivamente porqué no hay problemas con que n crezca (en este caso) que proposición o argumento general me asegura que no va a haber problema?

3) En que casos como el ejemplo puedo aplicar el ERP de solo un conjunto (por ejemplo aplicar solo el de Σ∗ aquí) y cuando es que el resto de parámetros pueden crecer sin que me cause problemas?

Re: Recursión en funciones con más de una variable definida de forma inductiva.

de Fernando Carpani - jueves, 19 de marzo de 2020, 17:16

Hola.

Una forma de ver el problema es tratar de escribir una funcion (por ejemplo, $f : \mathcal{N}\times \Sigma^* \to \Sigma^*$ que trate de seguir el esquema de recursión de $\Sigma^*$ pero que no pare o que nos devuelva dos valores para la misma pareja (viole la funcionalidad).

Saludos

FDO.