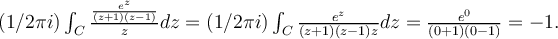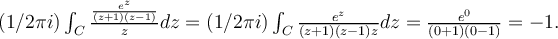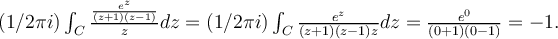
Si calculas la integral en una curva cerrada, la misma, por Green, será una combinación lineal de la integral en círculos alrededor de cada cero sin que pase por lo otros. Por ejemplo, si quieres calcular alrededor de z=0, alcanza con la circunferencia C de radio 1/2 y centrada en z=0. En el disco determinado por C, la función e^z/((z+1)(z-1)) es holomorfa, por lo que su valor en z=0, será, por Cauchy,