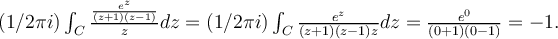Para hacer este ejercicio exprese el denominador de la integral como z(z+1)(z-1), entonces considere una función g(z) = e exp(z)/(z+1) si z <> -1 y lo mismo pero sobre z(z-1) si z <> 1. Se entiende?
Esto lo hice para aplicar el teorema de Cauchy, luego me queda que la integral es igual a 2pi(i).g(a). Discriminando según a sea 0, 1 y -1 y también dependiendo de como considere la curva gamma.
El problema que tengo es que g(a=0) no existe, puedo considerar g(a=0) = 0?
Es así que se resuelve el problema?
Gracias.
Esteban S.