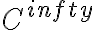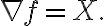alguien podria explicarme porque no es de gradientes? porque lo hice y me da que es de gradientes!
En respuesta a Nicolas Marcelo Cardenas Lopez
duda campo de gradientes
me di cuenta q tengo una duda teorica que por esto me tranco en algunos ejercicios... no estoy pudiendo darme cuenta si un campo es de gradientes o no... porque yo lo q hago es lo siguiente:
tengo X(x,y) = (ycos(x),xsin(y)) agarro y hallo:
f= integral(ycos(x)dx) y luego lo derivo y por obvio eso da fx=ycos(x)
f= integral(xsin(y)dy) y luego lo deviro y me va a dar y por obvio fy=xsin(y)...
y a (fx,fy) lo llamo gradiente de f pero por obvio esto es lo mismo que X...
si alguien me pudiera sacar me la duda de como hallar bien si un campo es de gradientes o no se lo agradezco! gracias
Un campo 
definido en 
es de gradientes si existe una función de clase 
tal que
En el caso de este ejercicio no existe tal
, una manera de probar esto es verificar que la integral de linea en alguna curva cerrada distinta a cero.
definido en es de gradientes si existe una función de clase tal queEn el caso de este ejercicio no existe tal
, una manera de probar esto es verificar que la integral de linea en alguna curva cerrada distinta a cero.
distinta de cero, salute
ya lo arregle en la respuesta...gracias jana!
gracias, arriba!
En respuesta a Jana Rodriguez Hertz
Re: duda campo de gradientes
no entendi mucho la parte de... "En el caso de este ejercicio no existe tal 
, una manera de probar esto es verificar que la integral de linea en alguna curva cerrada distinta a cero."
Pero creo q me encamine mas y a ver si esta bien lo q interprete...
tengo X(x,y) = (ycos(x), xsin(y))
hallo f(x,y) quedandome f(x,y) = ysin(x) - xcos(y)
y por lo tanto gradiente(f) = ( ycos(x) - cos(y) , sin(x) + xsin(y) )
y ahi si tengo que gradiente(f) es diferente a X.
estoy masomenos en lo cierto haciendo esto?
, una manera de probar esto es verificar que la integral de linea en alguna curva cerrada distinta a cero." Pero creo q me encamine mas y a ver si esta bien lo q interprete...
tengo X(x,y) = (ycos(x), xsin(y))
hallo f(x,y) quedandome f(x,y) = ysin(x) - xcos(y)
y por lo tanto gradiente(f) = ( ycos(x) - cos(y) , sin(x) + xsin(y) )
y ahi si tengo que gradiente(f) es diferente a X.
estoy masomenos en lo cierto haciendo esto?
Eso prueba que la hallada no es un potencial para el campo , eso NO implica que el campo no sea de gradientes. Revisa el teorema que da condiciones suficientes y necesarias para que un campo sea de gradientes, mira la dispositiva semana 5. La idea es probar que existe una curva cerrada tal que la circulacion del campo en dicha curva es distinta de cero, ergo el campo no puede ser de gradientes.
hallada no es un potencial para el campo , eso NO implica que el campo no sea de gradientes. Revisa el teorema que da condiciones suficientes y necesarias para que un campo sea de gradientes, mira la dispositiva semana 5. La idea es probar que existe una curva cerrada tal que la circulacion del campo en dicha curva es distinta de cero, ergo el campo no puede ser de gradientes.