Me surgió una duda con el ejercicio con carga q=kx2, como se considera la misma para hallar las reacciones?
Ademas, por qué los últimos dos no cumplen el teorema fundamental de vigas?
Gracias!
La idea de esa carga q es que es una función de x (el eje esta definido en el eje de la barra, comenzando en el apoyo izquierdo. La expresión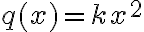 
representa una carga distribuida parabólica. Podes hacer equilibrio de momentos desde un apoyo teniendo en cuenta la carga q(x), y despues equilibrio vertical.
En la parte c) te pide que identifiques los casos donde no se cumple el teorema fundamental de vigas. El teorema establece que la derivada del momento es el cortante. Los dos casos donde hay un momento distribuido (m), no cumplen por lo tanto el teorema de vigas, ya que la derivada del momento es m y no V.
Muchas gracias! Lo único que sigo sin entender es como usar esa carga para el equilibrio vertical, porque con una carga distribuida uniformemente vos tomas la carga por el largo del tramo y cuando tenes una carga lineal tomas el area del triángulo, en este caso como sería?
En el caso de una carga q uniforme la resultante es: 
siendo eso el área de la carga
Análogamente 
por lo tanto es el área del triangulo
Entonces en el caso de que vos tengas cualquier tipo de carga en función de x (en este caso parabolica), la resultante va a ser:
si , entonces 
Ahora si entendi, gracias!