Buen día.
Hay algunos errores que voy a comentarte. Te recomiendo ir a alguna de las clases de consulta si no queda claro (porque es más fácil explicar en persona que en un foro).
Por una parte, el Principio de Inclusión-Exclusión no está bien aplicado ahí. Lo que hay que hacer es definir conjuntos para después restar cada uno, sumar las intersecciones de dos y restar la intersección de los 3. Una forma de aplicarlo bien sería considerando 3 conjuntos: 1: los que tienen 3 A seguidas en los primeros 3 lugares; 2: los que tienen 3 A seguidas en los lugares 2,3 y 4; 3: los que tienen 3 A seguidas en los últimos 3 lugares. Aplicando la fórmula con esos 3 conjuntos me parece que da bien. La diferencia con tu cuenta vendría a estar en la intersección de 1 y 3, que se cancela con la intersección de los 3.
Uno puede, también, contar los repetidos a mano, sin usar el principio de inclusión exclusión. Pensándolo de esa forma, el error que hay en tu razonamiento es que al caso de 5 A lo estás restando 2 veces. En los casos de 3 A seguidas lo restas 3 veces, en el caso de 4 A seguidas lo sumas 2 veces y en el último caso lo restas otra vez. En total estás quitándolo dos veces. El resto de los casos me parece que estás quitándolos solamente una vez.
Espero que te sea de utilidad. Si no te queda claro, nuevamente te recomiendo ir a alguna clase de consulta.
Saludos!
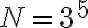número de palabras de largo 5 sin ninguna restricción. 
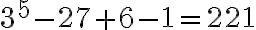(un caso menos que la solución correcta).