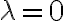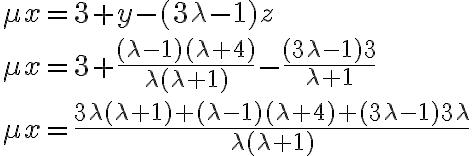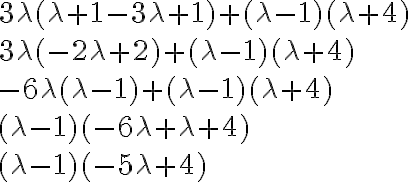Consultas

Buenos días,

Tenes razón Lucas, hice la cuenta con los signos cambiados. Pido las disculpas del caso.

En la discusión dice 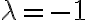$\lambda = -1$ el sistema es incompatible, eso es correcto.

Pero si 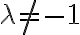$\lambda \neq -1$ no saben que pasa con el sistema.

Ahí pasan a la segunda ecuación y discuten con la variable y. Ese es el paso en el que están ahora.

$y = \frac{( \lambda -1 )( \lambda + 4 )}{ \lambda( \lambda +1 ) }$

En este punto saben que 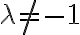$\lambda \neq -1$, por ese lado el y lo pueden obtener, pero tienen que abrir dos casos nuevos para discutir:

1- $\lambda = 0$

2- $\lambda \neq 0$ 

Si para algunos de esos casos la variable y esta determinada. Van a la ecuación 1 a determinar x.

$\mu x = 3 + y - (3 \lambda -1)z \\ \mu x = 3 + \frac{(\lambda - 1)(\lambda + 4)}{\lambda(\lambda + 1)} - \frac{(3 \lambda -1)3}{\lambda + 1}\\ \mu x = \frac{3\lambda(\lambda + 1)+(\lambda - 1)(\lambda + 4) + (3 \lambda -1)3\lambda}{\lambda(\lambda + 1)}$

Recuerden que si están trabajando en x, 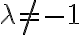$\lambda \neq -1$  y $\lambda \neq 0$ 

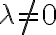
Ahora sacan factor común en el numerador:

$3\lambda(\lambda +1 -3\lambda + 1) + (\lambda - 1)(\lambda + 4)\\ 3\lambda(-2\lambda + 2) + (\lambda - 1)(\lambda + 4)\\ -6\lambda(\lambda - 1) + (\lambda - 1)(\lambda + 4)\\ (\lambda - 1)(-6\lambda + \lambda + 4)\\ (\lambda - 1)(-5\lambda + 4)\\ $

Acá la discusión tiene dos partes, no alcanza solo con decir que si 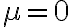$\mu = 0$ el sistema es indeterminado, hay que ver que pasa con numerador para completar esa afirmación.

Revisen las cuentas. Ya saben que puede fallar.

Si tienen más dudas estoy a las ordenes.

Manden la discusión, así vemos si están todos los cosos.

Saludos,

Bettina.