Hola betina tuvimos un problema con el problema 1 del segundo parcial de 2017, podrías mandar la solución y el procedimiento? Porque no sabes cuál es error, muchas gracias.
Buenas tardes Lucas,
¿Cuál fue el problema que tuvieron?
Para resolver el ejercicio deben comenzar con una escalerización gaussiana y luego empezar a discutir por casos.
¿Hicieron la escalerización? ¿Cómo les quedó?
Mi sugerencia para comenzar con ese ejercicio, es que la ecuación 3 la escriban como fila 1 de la escalarización.
En la primer columna tengo el mismo valor, así que la ecuación 2 la cambian por E2-E1, la ecuación 3 la cambian por E3-E1.
La ecuación 3 les queda múltiplo de 2, simplifiquen. Cambian la ecuación 3 por E3-E2 y tienen pronta la escalerización.
A partir de ese momento tiene que empezar a discutir por casos.
La última ecuación les queda algo del tipo  , entonces tienen que ver como queda el sistema cuando
, entonces tienen que ver como queda el sistema cuando  o
o  . Una vez terminan de discutir esos dos casos, si existe algún
. Una vez terminan de discutir esos dos casos, si existe algún 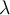 para el cuál el sistema tiene solución, tiene que ir a la segunda ecuación para seguir discutiendo.
para el cuál el sistema tiene solución, tiene que ir a la segunda ecuación para seguir discutiendo.
Si siguen trancados, adjunten una foto de lo que hicieron o hasta dónde llegaron, así la respuesta es más acotada.
Saludos,
Bettina.
El problema que se nos presento fue al resolver el valor de y, ya que no nos queda una raiz en el denominador igual a la del numerador por lo tanto no podemos cancelar nada y al hallar la x se vuelve algo muy complicado. Quizas cometimos un error por eso le dejo aqui nuestro procedimiento a partir de lo que me respondiste anteriormente (ya lo teniamos hecho). Muchas gracias por responder!
Hola Lucas,
Si van a buscar raíces no hagan distributiva en el denominador.
No sé cómo están buscando las raíces, pero el denominador tiene raíces 0 y -1, mientras que el numerador tiene raíz evidente -1 y la otra raíz tiene que ser 4.
Saludos,
Bettina.
Las raíces evidentes del numerador son el problema, y me parece que son 1 y -4 si no me equivoco ya que con -1 te queda -6 arriba. Nose cómo saco que el -1 es raíz evidente
Buenos días,
Tenes razón Lucas, hice la cuenta con los signos cambiados. Pido las disculpas del caso.
En la discusión dice  el sistema es incompatible, eso es correcto.
el sistema es incompatible, eso es correcto.
Pero si  no saben que pasa con el sistema.
no saben que pasa con el sistema.
Ahí pasan a la segunda ecuación y discuten con la variable y. Ese es el paso en el que están ahora.
En este punto saben que  , por ese lado el y lo pueden obtener, pero tienen que abrir dos casos nuevos para discutir:
, por ese lado el y lo pueden obtener, pero tienen que abrir dos casos nuevos para discutir:
Si para algunos de esos casos la variable y esta determinada. Van a la ecuación 1 a determinar x.
Recuerden que si están trabajando en x,  y
y 
Ahora sacan factor común en el numerador:
Acá la discusión tiene dos partes, no alcanza solo con decir que si  el sistema es indeterminado, hay que ver que pasa con numerador para completar esa afirmación.
el sistema es indeterminado, hay que ver que pasa con numerador para completar esa afirmación.
Revisen las cuentas. Ya saben que puede fallar.
Si tienen más dudas estoy a las ordenes.
Manden la discusión, así vemos si están todos los cosos.
Saludos,
Bettina.





