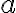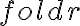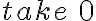ProgFunc: [Ejercicio autoevaluación] [Definiciones y tipos algebraicos] [Pregunta 2]

Estimados, tengo una duda en esta pregunta:

Dada la siguiente definición:

a = 1 : foldr (\x xs -> 1 + x : xs) [] a

¿Cuál es el resultado de evaluar take 4 a?

No entiendo por qué la solución es [1,2,3,4], ya que al hacer foldr el pliegue es por el último elemento de la lista, el cual se desconoce.

Entonces, para poder saber cuales son los primeros 4 elementos de la lista, primero necesito ir aplicando la función lambda entre el último elemento de la lista y el acumulador.

Agradezco si alguien me puede indicar si estoy pensando el problema de forma errónea.

Re: [Ejercicio autoevaluación] [Definiciones y tipos algebraicos] [Pregunta 2]

de Juan Pablo García Garland - martes, 14 de mayo de 2019, 19:16

Este ejercicio se nos coló, y en realidad trata del tema evaluación perezosa, que se introdujo hoy en el teórico (aunque un poco se viene hablando de ella desde el comienzo del curso).

$a$ es una lista infinita, pero la gracia es que al llamar

$take \: 4$ con ella como argumento, solo necesitamos producir 4 valores.

En ejercicios de este estilo algo que se puede hacer es hacer la reducción (en call by name) y ver que va pasando. Uso

$>>>$ para mostrar reducciones (no necesariamente un paso)

take 4 a  
>>> take 4 (1 : foldr (\x xs -> 1 + x : xs) [] a) 
>>> 1 : take 3 (foldr (\x xs -> 1 + x : xs) [] a)

Aca

$take$ necesita la cabeza de la lista, para eso el

$foldr$ tiene que producir,

el redex de más afuera es recién

$a$ que tenía su regla de rescritura, seguimos:

>>> 1 : take 3 (foldr (\x xs -> 1 + x : xs) [] (1 : foldr (\x xs -> 1 + x : xs) [] a)) 
>>> 1 : take 3  (1 + 1 : foldr (\x xs -> 1 + x : xs) [] (foldr (\x xs -> 1 + x : xs) [] a))
>>> 1 : 1 + 1 : take 2 ....

Se ve? Cuando lleguemos a

$take \: 0$ tiramos todo el argumento feo que viene, y devolvemos la lista resultante. El paso anterior de reducción es algo así como

1 : 1+1 : 1+1+1 : 1+1+1+1 : take 0 (...)

Re: [Ejercicio autoevaluación] [Definiciones y tipos algebraicos] [Pregunta 2]

de Hugo Sebastian Rodriguez Reyes - martes, 14 de mayo de 2019, 21:26

Gracias por la respuesta.

Entiendo la idea, pero me es difícil identificar que es el resto de la lista a la que le aplico nuevamente foldr, y como tengo que generad un nuevo valor con a para poder calcular nuevamente el valor que necesito.