Re: Ejercicio 5 - Hoja de ejercicios adicionales
![x[n]=\delta[n] x[n]=\delta[n]](https://eva.fing.edu.uy/filter/tex/pix.php/e0c9cacc38fb9ce6fccb1f5fd6fe1275.gif) con la salida en reposo
con la salida en reposo ![y[-1]=0 y[-1]=0](https://eva.fing.edu.uy/filter/tex/pix.php/d30da34395c2e49e9786d4c686f19aeb.gif) (esto lo sabemos al ser el sistema causal) y viendo cómo queda la salida para
(esto lo sabemos al ser el sistema causal) y viendo cómo queda la salida para 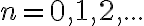 . Por ejemplo, para
. Por ejemplo, para 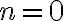 y
y 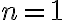 se tiene
se tiene ![y[0]= \mu y[-1]+\lambda x[0]=\lambda y[0]= \mu y[-1]+\lambda x[0]=\lambda](https://eva.fing.edu.uy/filter/tex/pix.php/688061080420b33ebc75118da0cc9870.gif) y
y ![y[1]=\mu y[0]+\lambda x[1]=\mu\lambda y[1]=\mu y[0]+\lambda x[1]=\mu\lambda](https://eva.fing.edu.uy/filter/tex/pix.php/282ad138ce7ff7cae6c7a1dbc5de774f.gif) . Si se sigue por inducción completa se llega a
. Si se sigue por inducción completa se llega a ![h[n]=u[n]\lambda \mu^n h[n]=u[n]\lambda \mu^n](https://eva.fing.edu.uy/filter/tex/pix.php/d887be51ea0f24b2d6dc87160ed7eb32.gif) . Esta forma de obtener
. Esta forma de obtener ![h[n] h[n]](https://eva.fing.edu.uy/filter/tex/pix.php/76df30cb2f3c2675e057e25429917f27.gif) vale para cualquier valor de
vale para cualquier valor de 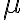 y
y 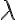 .
.Usar la DTFT para obtener la respuesta al impulso de la ecuación en diferencias solo es válido bajo la hipótesis de que exista la DTFT, y una condición suficiente para que esto pase es que la respuesta al impulso sea absolutamente sumable. Pero ésta es justamente la condición para que un SLIT sea estable. Por lo tanto puede usarse la DTFT si se sabe que el sistema es estable. Uno podría también poner la estabilidad como hipótesis y comprobarla luego.
En el caso de arriba el sistema es estable para 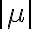 como bien planteaste. Si
como bien planteaste. Si 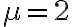 u otro valor de modulo mayor a uno, entonces la respuesta al impuso
u otro valor de modulo mayor a uno, entonces la respuesta al impuso ![h[n]=\lambda \mu^n h[n]=\lambda \mu^n](https://eva.fing.edu.uy/filter/tex/pix.php/738987f6348927aea8548deb7b83e0d8.gif) no es absolutamente sumable (ni siquiera es acotada), por lo que el sistema no es estable y tampoco converge la DTFT. Pero
no es absolutamente sumable (ni siquiera es acotada), por lo que el sistema no es estable y tampoco converge la DTFT. Pero ![h[n]=\lambda \mu^n h[n]=\lambda \mu^n](https://eva.fing.edu.uy/filter/tex/pix.php/738987f6348927aea8548deb7b83e0d8.gif) sigue siendo la respuesta al impulso ya que la obtuvimos directamente sin usar la DTFT ni la hipótesis de estabilidad.
sigue siendo la respuesta al impulso ya que la obtuvimos directamente sin usar la DTFT ni la hipótesis de estabilidad.
Espero que esto aclare la pregunta. Cuando veamos la transformada 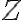 más adelante en el curso tendremos más herramientas para antitransformar sistemas no estables y estudiar casos más generales.
más adelante en el curso tendremos más herramientas para antitransformar sistemas no estables y estudiar casos más generales.
Saludos
Juan Bazerque
