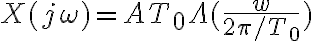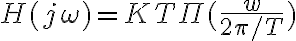ejercicio 7 practico 4

ejercicio 7 practico 4

de Ilana Stolovas Rostkier -
Número de respuestas: 7
Hola, en el practico de transformada de fourier en tiempo continuo , el ultimo ejercicio plantea:

-x(t) = A sinc^2(t/To)

-n(t) = B sin(16pi*t/To)

-xn(t) = x(t) + n(t)

-h(t) = K sinc(t/T) (la respuesta al impulso a traves de un SLIT invariante en el tiempo)

Se pide hallar T para que la respuesta del sistema ante la entrada xn(t) sea x(t).

Planteando los datos llego a la ecuacion en transformadas: X(jw) = [X(jw)+N(jw)]*H(jw)

Sin embargo, transformar las señales para resolver esa ecuacion resulta engorroso (pasando el sinc a sen y luego a exponenciales, o usando la tabla de transformadas). en especial para x(t).

Hay otra forma de resolver el ejercicio? O alguna recomendacion para plantear las transformadas?

Gracias

En respuesta a Ilana Stolovas Rostkier

Re: ejercicio 7 practico 4

de Gaston Garcia Gonzalez -

Buenas Ilana,

la transformada de los sinc's en el tiempo se puede sacar por dualidad, no es necesario hacer el pasaje que dijiste. Recién acabamos de publicar la hoja de formula donde aparecen estas transformadas. También la podes encontrar al principio del Capitulo 5 del libro.

Saludos.

En respuesta a Gaston Garcia Gonzalez

Re: ejercicio 7 practico 4

de Ilana Stolovas Rostkier -

No entendi bien como aplicar dualidad en este caso. Tengo la transformada de la tabla que aparece en la imagen. Como puedo hallar a partir de ella la transformada de x(t)=Asinc^2(t/To)?

Gracias


Adjunto Imagen1.png
En respuesta a Ilana Stolovas Rostkier

Re: ejercicio 7 practico 4

de Santiago Martinez -

Hola, no sé exactamente dónde radica tu duda. Tal vez una fuente de dudas son las variables: el sinc(t/To) habria que escribirlo como sinc(w/wo). En tu caso wo valdría 2pi/Tau.

Si la duda no es esa seguimos por este hilo.

Saludos.


En respuesta a Santiago Martinez

Re: ejercicio 7 practico 4

de Juan Santiago Garcia Pose -

Buenas, en ese ejercicio también tengo una duda, y es que cuando hallo las transformadas me quedan distinto que en la solución.

A mi me quedaron  X(j\omega) = AT_{0} \Lambda (\frac{w}{2\pi/T_{0}})   ,  H(j\omega) = KT \Pi (\frac{w}{2\pi/T}) . Sin embargo en la solución se omite la constante K y las constantes T_o y T respectivamente (capaz yo le erré al aplicar dualidad, que puede ser muy probable). Pero suponiendo que mis resultados están bien, además de las cotas inferiores y superiores que dice la solución para T, ¿no queda directamente definido T si hay que considerar que el producto KT = 1 ? Para que no se altere la amplitud de X(jw). Eso es lo que me está mareando. Espero me haya hecho entender. 


Saludos
En respuesta a Juan Santiago Garcia Pose

Re: ejercicio 7 practico 4

de Santiago Martinez -

Mirando la solución, faltan las constantes que mencionas. Gracias.

Tu razonamiento parece correcto, es decir que habría una restricción "muy dura" para obtener sólo x(t). La idea del problema es observar que uno puede obtener x(t) "amplificada" por una constante (que como vos evidencias, depende del filtro).

Con la letra cómo está deberías imponer la restricción que comentás.

La verdad es que la letra debería decir algo como "diseñar la constante para NO obtener n(t) en la salida del filtro".

Actualizaremos la letra y la solución para preguntar lo interesante y corregir los errores.


Muchas gracias y espero te sirva la respuesta.