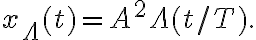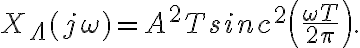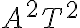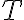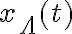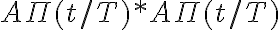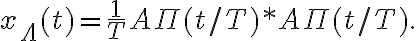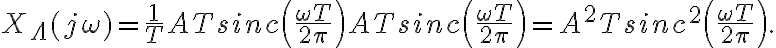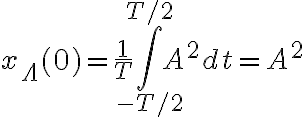Hola, el viernes un compañero (creo que se llama Santiago igual que yo) preguntó por qué al hacer la convolución con cuentas de los dos pulsos daba 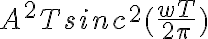 y cuando se hizo en el pizarrón como el producto de las dos convoluciones de los pulsos daba
y cuando se hizo en el pizarrón como el producto de las dos convoluciones de los pulsos daba 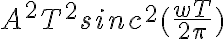 . El problema era que en realidad la convolución de dos pulsos rectangulares es:
. El problema era que en realidad la convolución de dos pulsos rectangulares es: 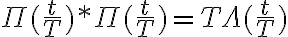
De ahí es que cuando se hizo en el pizarrón sobraba un T.
PD: Paso por ventanilla a retirar los puntos para el parcial por escribir con ecuaciones y todo o cómo hacemos?