Me preguntaron este ejercicio que aparecio en la prueba
Sea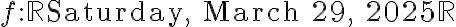 
una función derivable en 
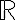se sabe que una primitiva de 
es la función 
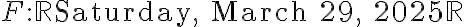definida por
Calcule:
Aplicando partes
Hola! Yo también tengo una duda de este ejercicio.
Por partes porque no queda 
?
No pude resolver este ejercicio porque la ultima integral me quedo imposible.
Gracias!
Claro, esa misma es mi duda. A mi también me queda que y no que en la resta (en la integral) es f(x). Porque si tomas f(x) como la que está derivada (en la primera ecuación) en las siguientes dos partes, es F(x).
Yo también tengo esa duda, no lo pude hacer, me quedaba un integral re larga, y me complico resolverla, y ahora no entiendo lo de F(x) que aparece en esa formula que pasaron?
Profe en la segunda integral, si aplicas partes te quedaria la integral de
F(x), no la integral de f(x), y no conocemos una primitiva de F(x)
El El lun, 26 de nov. de 2018 a las 14:11, Carolina Puppo (vía FING) <
F(x), no la integral de f(x), y no conocemos una primitiva de F(x)
El El lun, 26 de nov. de 2018 a las 14:11, Carolina Puppo (vía FING) <
Tienen razón!! Les pido disculpas y les agradezco
las explicaciones !
Luego les acredito los puntos de esta pregunta a todes
Muchas gracias!!
gracias :)
Hola, en este ejercicio también pasaba lo mismo
Si paso en varais versiones les adjudicamos los puntos por eso a los que les toco
Verifiquen en la tabla y por reclamos lo hacen en el lugar correspondiente ^_^