hola quisiera saber si esta funcion f(z)= |z| (ro o norma) es diferenciable???
yo llegue a q no xq si me muevo en el sentido de z mi derivada es positiva la distancia aumenta pero si me muevo en contra es negativa y en teoria no deberia depender de esto
Matematicamente solo llegue a q tenia una norma entre -1 y 1 pero este agurmento hablado me parecio bastante intuitivo aunque no me da seguridad si estoy bien en los calculos gracias
creo es el ej 2.4-a
Hola, la función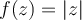 
es diferenciable (entendemos diferenciable como la noción clásica de 
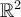) en todo punto a excepción de z = 0. Podés calcular las derivadas parciales y notar que es clase 
.
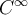La cosa es ver si es derivable como función compleja (holomorfa), para responder esa cuestión, ya tenemos que es diferenciable en todo punto menos 0. Si vemos a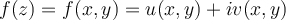
, u y v ¿satisfacen las ecuaciones de Cauchy-Riemann? Si es así, eso implica que es derivable. En caso contrario no lo será.
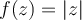es diferenciable (entendemos diferenciable como la noción clásica de 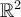) en todo punto a excepción de z = 0. Podés calcular las derivadas parciales y notar que es clase 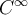. La cosa es ver si es derivable como función compleja (holomorfa), para responder esa cuestión, ya tenemos que es diferenciable en todo punto menos 0. Si vemos a
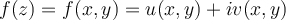, u y v ¿satisfacen las ecuaciones de Cauchy-Riemann? Si es así, eso implica que es derivable. En caso contrario no lo será.
El teorema no dice que si es derivable entonces se dan las ecuaciones de C- R ?
El teorema que demostramos en el teórico y que sirve para ese ejercicio dice que "f(z) es homomorfa en un punto interior z_0 si y solo si su parte real e imaginaria son diferenciables en en z_0 y cumple C-R."
Saludos,
Eduardo