Alguien podría explicar o dar una idea sobre el ejercicio 3 del práctico 1?
No entiendo la definición de a1 equivalente con a2.. que es (mod 2pi)?
Se puede "ver" gráficamente la definición?
Gracias.
Esteban S.
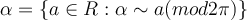 ?
?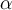 al conjunto antes mencionado Y TAMBIÉN al número real que incluye en la definición de dicho conjunto?
al conjunto antes mencionado Y TAMBIÉN al número real que incluye en la definición de dicho conjunto?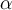 ?
?