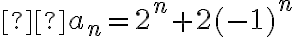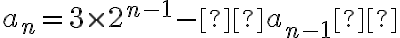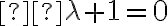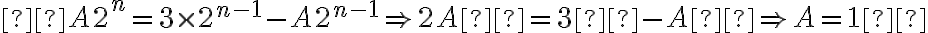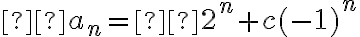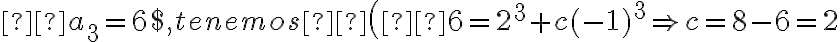Novedades

Hoy en el teórico vimos el problema de la ruleta, y un estudiante sugirió considerar cuando el primer casillero y el último son iguales. 

En clase lo interpreté de una forma agregando un casillero, pero al final de clase él me dijo que pensaba el problema sin agregar un casillero. Parece que me quedó la idea rondando la cabeza y se me ocurrió una solución que termina dando una ecuación lineal no homogénea de 1er orden. Esto no es extraño, es parte de un fenómeno más general que no vemos en este curso pero que ocurre.

A continuación va la solución:

Hallar la cantidad de  formas  de pintar una ruleta de $n$ números con tres colores, de forma tal que números adyacentes tengan color distinto.

Si pintamos sin importar que el primero y el último sean distintos tenemos 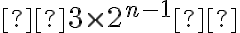 $3\times 2^{n-1}$ formas.

Para hallar la cantidad  $a_n$ deseada, debemos restar los casos en que el primero y el último son iguales, pero esos casos son 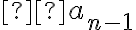 $a_{n-1}$, por lo tanto 

$a_n =3\times 2^{n-1} -  a_{n-1}$.

Es una ecuación de 1er orden no homogénea, con ecuación característica 

$\lambda+1 = 0$.

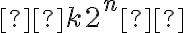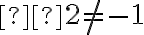Como el término independiente es de la forma  $k2^n$ y  $2\neq -1$, sabemos que existirá una solución particular de la forma  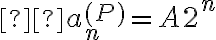$a_n^{(P)} = A 2^n$. Para hallar A sustituimos en la ecuación:

$A 2^n =3\times 2^{n-1} - A 2^{n-1} \Rightarrow 2A  =3  - A  \Rightarrow A =1$

De donde la solución general es  $a_n =  2^n +c(-1)^n$.

Como $a_3 = 6$, tenemos  \( 6 = 2^3 +c(-1)^3 \Rightarrow c = 8-6=2$, y la solución será $a_n = 2^{n} +2(-1)^n$