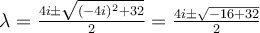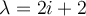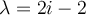Hola, tengo un problema para calcular los vaps y es que cuando hago el determinante de b(T)b-lambda*I me queda una ecuación con i, como se hallan los valores propios en ese caso? Porque por lo general cuando los ejercicios tienen complejos en la ecuación del determinante quedan los i al cuadrado y al final la ecuación queda con lambda y reales, gracias!
Hola que tal,
Si no me equivoco el polinomio característico queda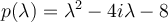 
, ahora, como me gusta mencionarles en clase, a groso modo lo único que se pierde en trabajar con complejos es la noción de orden que en los reales si teníamos. La manera en que se operan los complejos es la misma, (y en general cualquier cuerpo algebraico cuenta con las mismas propiedades a la hora de operar), debido a esto es que sigue valiendo la formula de Baskara, la cuenta sería como sigue
Lo anterior da dos raíces, 
y 
Espero haberme expresado claramente,
Saludos!