Hola a todos,
Antes que nadas, les pido disculpas a quienes han planteado preguntas por este medio. Creí que estaba suscrito pero veo ahora que no. He atendido muchas consultas por correo y personalmente, pero veo que muchos han preguntado sólo por este medio.
En todo caso, las preguntas han sido muy similares, y creo que ameritan una serie de aclaraciones y explicaciones comunes que pueden ayudarles a todos.
Los tres temas que voy a tratar son
1) Spectral Clustering y Matrix Lasso
2) Cómo evaluar el funcionamiento y la convergencia correcta de algoritmos de optimización
3) Cómo funciona ADMM, y qué rol juega el parámetro "mu" que acompaña al término de penalización cuadrática en su convergencia.
4) buenas prácticas al depurar algoritmos de optimización
Para esto hice tres dibujos que adjunto. Voy a hacer referencia a los tres dibujos.
Sobre 1:
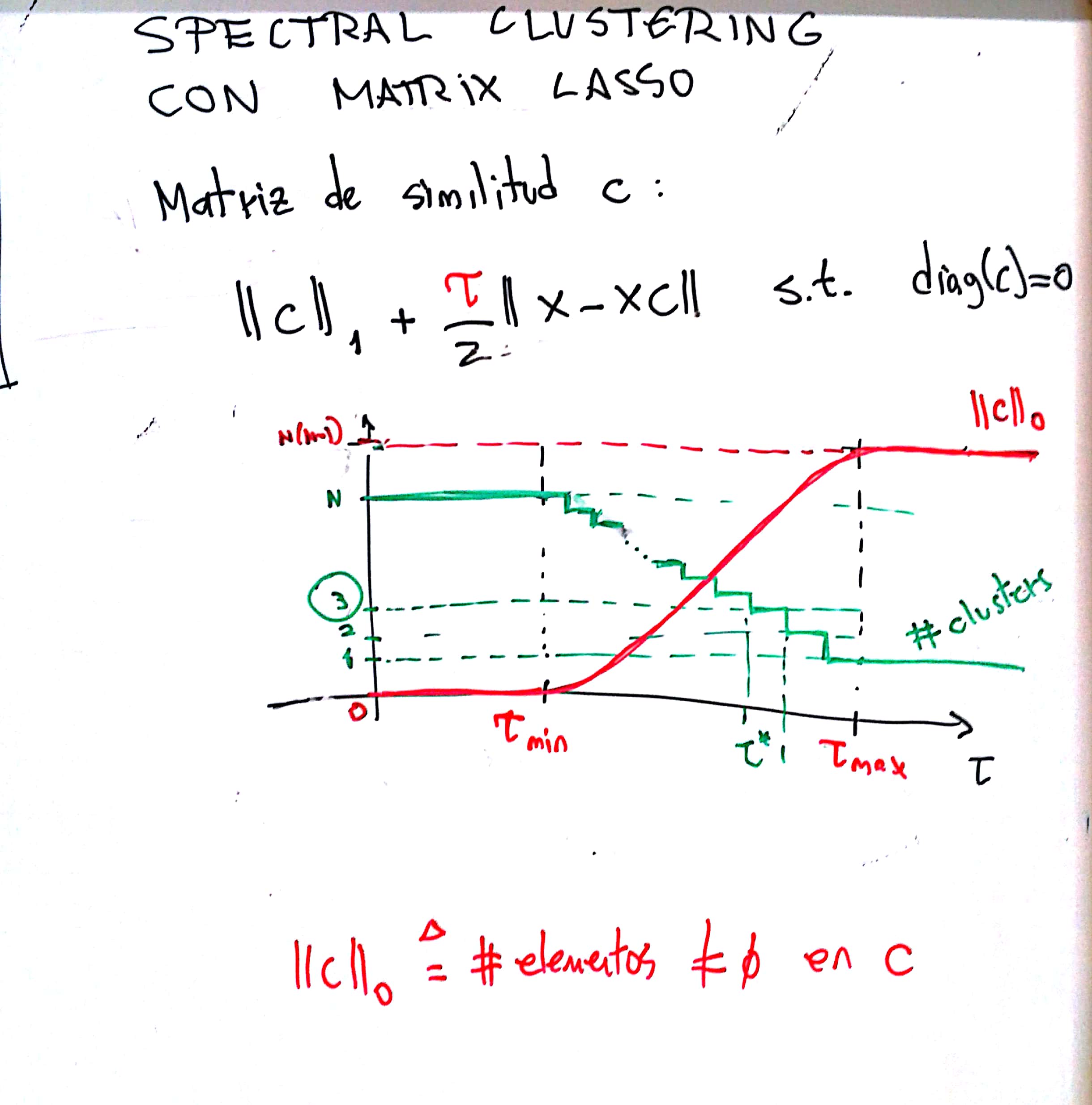
Spectral Clustering en general se basa en una matriz C de similaridad entre las columnas de X. En el caso de que se utilice, como se sugiere en el libro, el algoritmo Matrix Lasso, es muy importante que entiendan que el parámetro "tau" del Lasso es CRUCIAL para que la matriz C sea buena a los efectos de hacer SC.
Spectral clustering, idealmente, encuentra K subgrafos disjuntos mediante el análisis espectral del Laplaciano de C. El rol de tau es hacer C más o menos esparsa, y mientras más esparsa es C, más grupos habrán. Los casos límite son que C sea toda ceros (o sea, se tienen tantos clusters como muestras) o que sea totalmente densa (Salvo la diagonal) en cuyo caso se tiene UN cluster. Como muestra el dibujo, entonces, hay un rango útil de valores de "tau" en donde hay que jugar para que C tenga la cantidad ideal de conjuntos disjuntos. Eso no queda más remedio que buscarlo. Como en este caso sabemos la cantidad de clusters, podemos buscar ese tau inteligentemente hasta que de K=3 clusters y luego proceder a SC.
Sobre 2:
Muchos han venido con dudas sobre la convergencia de los algoritmos. En particular, pasó repetidamente que los algoritmos estaban bien implementados, pero la condición de parada estaba mal elegida de modo que el algoritmo se detenía muy prematuramente.
Es importante entender en optimización que el criterio de parada es FUNDAMENTAL, y no sólo eso, sino que depende de qué es lo que quiere uno sacar del problema. Importa el valor final de la función de costo o su argumento? Si el problema fuera uno de reducir costos monetarios, sin duda nos importaría lo primero. Pero en genera, y en particular en este curso, importa más el *argumento*. En ese caso, lo que hay que monitorear como condición de parada es la variación relativa del argumento (ver dibujo).
También se puede monitorear la velocidad de convergencia del algoritmo viendo cómo varía la variación (valga la redundancia). Normalmente uno esperaría en este caso que dX(t+1)/dX(t) ~ dX(t)/dX(t-1) (convergencia llamada "lineal"), o sea, que la variación del argumento se reduzca más o menos en la misma proporción con cada iteración. ES de esperar que en realidad esta sea mayor al principio.

Sobre 3:
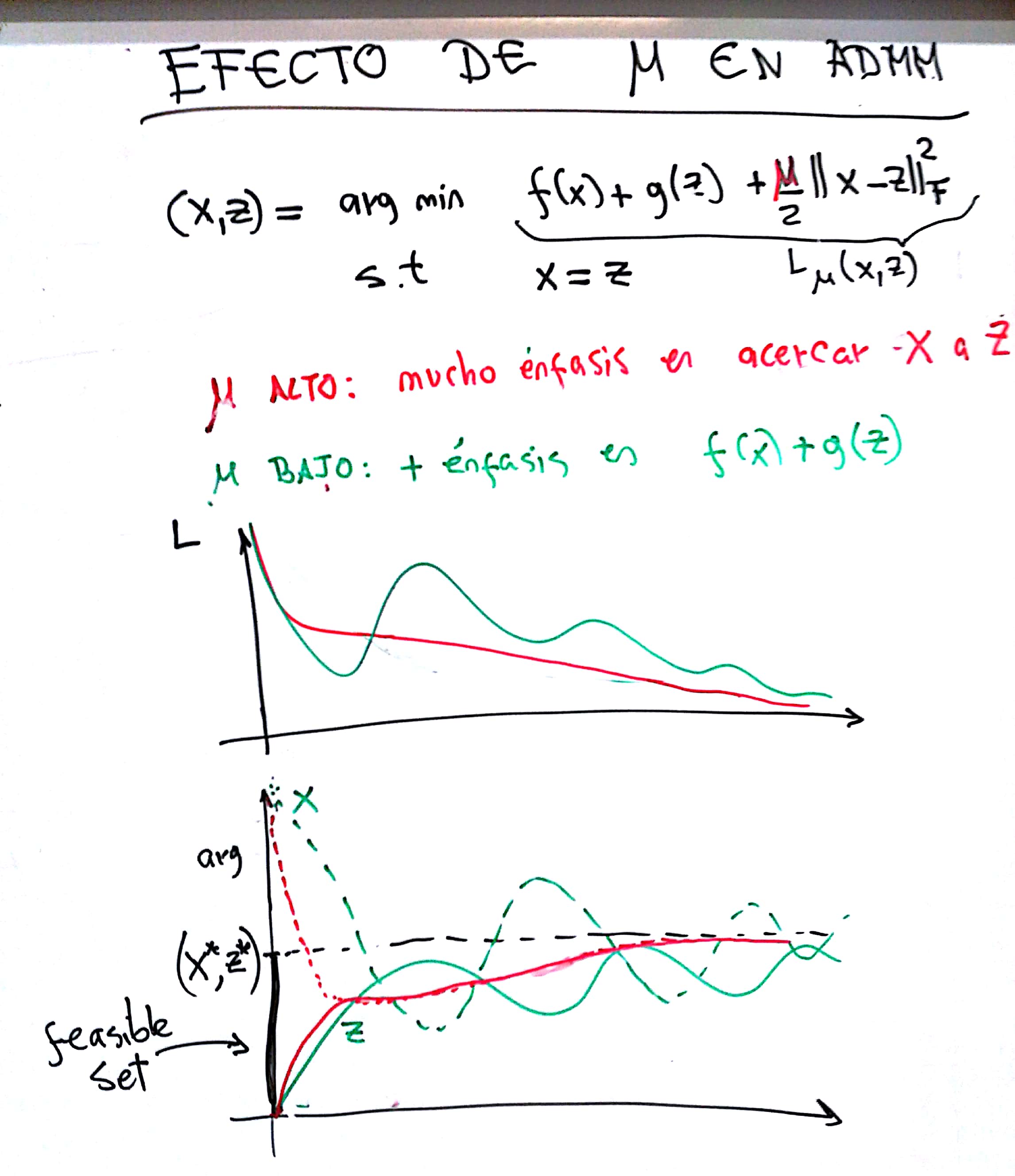
ADMM es un algoritmo muy muy fácil de implementar, pero elegir mu puede ser miserable. LO que hay que entender de ADMM es que mu regula qué tan importante es para el algoritmo que haya coincidencia entre las dos "copias" de la variable objetivo (X y Z en el dibujo). Lo otro que está bueno tener en cuenta es que el multiplicador de Lagrange hace de "integrador": acumula la discrepancia entre X y Z alo largo de las iteraciones.
De esto salen dos cosas:
1) si mu es muy bajo, las variables cambian de valor violentamente pero tienden a no acercarse mucho y el comportamiento es más bien errático. A la larga converge, pero estas oscilaciones demoran la covnergencia. Eso se ve en la evolución de la función de costo por ejemplo.
2) si mu es muy alto, las variables se acercan en seguida. Eso por un lado es bueno, pero por otro hace que la evolución ulterior del algoritmo sea muy lenta (el mult. de Lagrange queda esencialmente constante).
Estas dos cosas se muestran el el tercer dibujo que adjunto.
El punto ideal de mu está en el medio, y es un arte buscarlo. Les recomiendo que prueben valores en una escala logarítmica, desde 0.01 a 1000 por ejemplo.
4: buenas prácticas al depurar algoritmos de optimización
Es muy importante que "sepan lo que está pasando" en cada iteración.
Impriman, en cada iteración, valores relevantes del problema, como la variación de las variables, la función de costo. Impriman al principio el valor de los parámetros, etc.
Un ejemplo: en Lasso, como les decía, hay un tau mínimo a partir del cual la solución C es EXACTAMENTE 0. Eso se ve fácilmente en las iteraciones si ven que el valor máximo absoluto del argumento del Soft Thresholding es menor que el umbral de ST, entonces obviamente la salida del ST va a ser toda 0. Eso no suele ser bueno.
Pero sobre todo, impriman la variación relativa de las variables, su diferencia. En el caso de ADMM, conviene monitorear el multiplicador de Lagrange: si tiene a crecer mucho y se hace mucho más grande (en norma frobenius o valor máximo) a las variables objetivo, es que las variables no se acercan lo suficiente. Si es muy chico respecto a los argumentos, es que mu es demasiado grande.
Ahora voy a ver si puedo responder algunas de las preguntas del foro.
