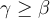Seay
dos subconjuntos de n\'umeros reales tales que existen
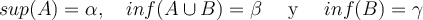 Considere las siguientes afirmaciones:
Considere las siguientes afirmaciones:Esas eran las afirmaciones a discutir.
1.donde la primera desigualdad es porque
y la segunda por definición de ínfimo y supremo. Entonces la primera afirmación es verdadera.
2. Para que la afirmación sea verdadera hay que probar que:lo cual es verdadero porque
y tambien hay que probar que
lo cual es verdadero analogamente. Luego la afirmación dos es también verdadera.
3 La tercera afirmación dicey esto tambiés es verdadero porque
.
Fijate que lo que necesitabas es saber esta propiedad :
Sientonces
y
.
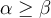
![A\cap B\subset [\gamma,\alpha] A\cap B\subset [\gamma,\alpha]](https://eva.fing.edu.uy/filter/tex/pix.php/0523a39fd902087a599b3f71586bcffa.png)