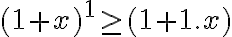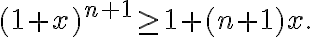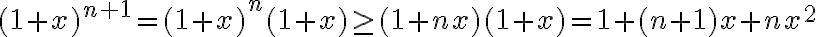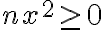Hola. Alguien podría decirme como se resuelven los ejercicios con desigualdades de inducción completa del practico 6. Gracias
Hola Martin te voy a explicar el ejercicio 2.2a del práctico 6.
Este ejercicio pide probar por inducción completa que para todo 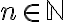 que
que
Para el paso base evaluamos la expresión para el caso 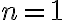 y verificamos que se cumple:
y verificamos que se cumple:
Para el paso inductivo suponemos que 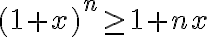 para un
para un 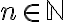 y queremos probar que
y queremos probar que
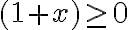 entonces usando la hipótesis inductiva :
entonces usando la hipótesis inductiva : Con lo que hemos probado el paso inductivo. Entonces por inducción completa podemos afirmar que
Muchisimas Gracias