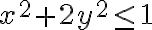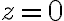hola, no entiendo como resolver el ejercicio, precisaria hallar una parametrizacion de dicha superficie, pero no logro encontrarla, si alguien me puede dar una mano, saludos
Re: ejercicio 4 practico 6
Lo primero que tenés que hacer es acomodar la ecuación de la elipse para tenerla en la forma  para poder reconocer el centro
para poder reconocer el centro 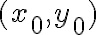 y los parámetros de los semiejes
y los parámetros de los semiejes 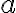 y
y 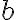 . Queremos saber esto porque la parametrización de la elipse en
. Queremos saber esto porque la parametrización de la elipse en 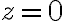 es
es 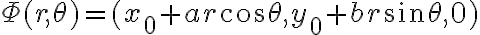 .
.
Si haces las cuentas vas a obtener que la ecuación para la elipse 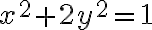 es equivalente a
es equivalente a 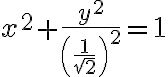 , entonces la parametrización en
, entonces la parametrización en 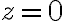 es
es 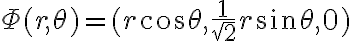 .
.
Vos no querés hacer la elipse en 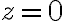 , la querés sobre el plano, o sea (despejando de la ecuación del plano) en
, la querés sobre el plano, o sea (despejando de la ecuación del plano) en 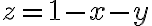 , que si reemplazas
, que si reemplazas 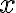 e
e 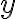 por las ecuaciones de
por las ecuaciones de 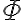 te queda
te queda 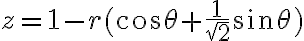
Por último querés la elipse entera, es decir ![\theta \in [0,2\pi] \theta \in [0,2\pi]](https://eva.fing.edu.uy/filter/tex/pix.php/69747d2f51c333c49b109690ee100d26.gif) , y si sustituyes
, y si sustituyes 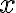 e
e 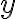 en
en 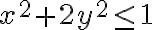 por las ecuaciones de
por las ecuaciones de 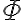 , vas a obtener que
, vas a obtener que 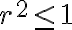 , que por tratarse de un radio (valor positivo) nos deja
, que por tratarse de un radio (valor positivo) nos deja ![r \in [0,1] r \in [0,1]](https://eva.fing.edu.uy/filter/tex/pix.php/88e1dec1d6ad5e2dbeebc8e4cc596159.gif) .
.
En resumen, la parametrización de la elipse "flotando" en 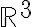 es:
es:
Saludos.