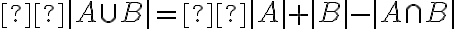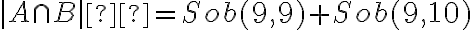Buenas, no entiendo de dónde sale el 2Sob(10,9) de la solución, ya que, si se aplica el principio de inclusión-exclusión, para hallar las funciones Sob tal f(1)=1 o f(2)=1, habría que hacer las que f(1)= 1 + f(2)=1 - las que f(1)=f(2)=1
Quedaría: Sob(10,10) + Sob(10,10) - Sob(9,9)
Me estaría faltando el Sob(10,9)
Te falta el caso en el que una condición se cumple necesariamente. Todos los que cumplen una o la otra = Todos los que NO cumplen la condición + Todos los que cumplen una condición - Todos los que cumplen ambas a la vez. Como tenés dos casos, podés decidir entre B y C.
Sob(10, 10) sería si el 1 tiene más de una Pre imagen, pero podría tener una sola.
Hola, estoy en la misma que el compañero estuvo, excepto que yo no apliqué el principio inclusión-exclusión. Lo que hice fue tomar f(1)=1 y "apartarlo" quedándome el dominio con 10 elementos, lo que corresponde a sob(10,10), lo mismo hice con f(2) que corresponde a otro sob(10,10), pero al hacer esto conté dos veces las funciones donde f(1)=f(2)=1, por lo que saqué del dominio a {1,2} y a {1} del codominio ya que ningún otro valor del dominio podría tomar el valor 1 (sino la función no podría ser sobreyectiva), por lo tanto me quedó un dominio de cardinal igual que el codominio que es 9 y la cantidad de funciones tal que f(1)=f(2)=1 corresponden a sob(9,9) y se lo resté al resultado que tenía, quedándome 2sob(10,10) - sob(9,9), y por más que lea una y otra vez los comentarios no puedo entender de donde sale el 2sob(10,9).
Me podrían dar una mano?
Gracias!
Sea A la condicion f(1) = 1, y B f(2) =1,
entonces 
(*)
|A| = Sob(10, 9) + Sob (10,10) porque distinguís si la preimagen de 1 es solo 1 o es 1 y otros elementos
|B| = |A|
por lo mismo, pero Sob(9,10) = 0 (podría no haberlo escrito).
Sustituyendo en (*) obtienen el resultado.
Saludos