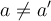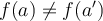Foro de Consultas

Hola Esteban 

Espero que estes mejor y hallas coseguidos las notas.

La definición de funcion que usas es correcta:

Considera 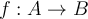$f:A\to B$ una correspondecia, es una función si a cada elemento del dominio A le corresponde un único elemento del codominio B.

Lo que no está bien es la definición de inyectividad y la de sobreyectividad..

Una función es inyectiva si dados dos elementos diferentes de A las imagenes también son diferentes, lo que es lo mismo que

$a\neq a'$ entonces $f(a)\neq f(a')$

Una funcion es sobreyectiva si todo elemnto del codominio B es imagen de alguien del dominio A, lo cual es lo mismo que:

Parar todo 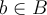$b\in B$ existe un elemento $a$ de $A$ tal que $f(a)=b$.

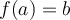Algunos ejemplos para refelxionar:

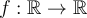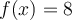1. $f:\mathbb R\to\mathbb R$, $f(x)=8$          Es  una funcion pues cada elemento del del dominio le corresponde un elemento del codominio. Por otro lado no es sobreyectiva pues por ejemplo el 3 es un elemento del codominio que no es imagen de ningún elemento del dominio. Tampoco es inyectiva pues dados dos elementos del  dominio, sus imagenes son la misma: 8.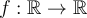
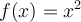2. $f:\mathbb R\to\mathbb R$  $f(x)=x^2$ es una función que no es inyectiva pues 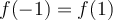$f(-1)=f(1)$ y tampoco es sobre porque por ejemplo $-1$ no es imagen de ningun numero. Sin embargo podemos restringir el dominio y el codominio y esto cambia. 
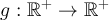
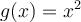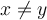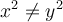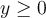3. Considera ahora $g:\mathbb R^+\to\mathbb R^+$ $g(x)=x^2$ está funcion es inyectiva y sobreyectiva. Para la inyectividad dados dos numeros positivos $x\neq y$ entonces $x^2\neq y^2$. Por lo tanto $f$ es inyectiva. Para la sobreyectividad, dado un $y\geq 0$ se tiene que si tomo 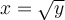$x=\sqrt y$ entonces $g(x)=y$.  

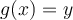Espero que te halla aclarado el panorama te recomiendo hacer los ejercicios en este orden:

Ejercicio 1.1

Ejercicio 1.3

Ejercicio 1.4

Estudiar composición y hacer ejercicios

Ejercicios 3.4 y 3.5

Saludos