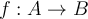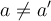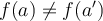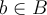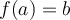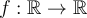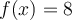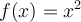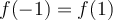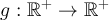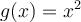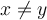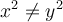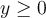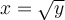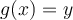Quería saber si pueden mandar por este medio los ejercicios y las soluciones de lo que hagan hoy en el práctico de las 16 ya que no voy a poder asistir porque ando bastante engripado
Si alguien no le molesta mandarme fotos de los ejercicios dejo mi celular 098790944
Otra cosa es, que gustaría sacarme bien la duda sobre función sobreyectiva porque no logro asociar bien el concepto en la expresión analítica, ejemplo en el ejercicio 4 del práctico 3
Y en el ejercicio 3 de los bosquejos graficos también...
Corregirme si me equivoco :
- Función es siempre y cuando a un elemento del dominio le corresponde solamente un elemento en el condominio?
- Inyectiva es si a lo sumo tengo un elemento en el dominio correspondiente a uno del condominio?
O sea a cada f(x) le corresponde una x???
- y sobreyectiva sería que le corresponde una o más de una x a cada f(x)????
O sea x puede tomar mas de un valor para el mismo f (x)???
Gracias por la ayuda
Saludos