Buenas, estoy trancado en este ejercicio (Feb2015 ej 4), planteando la divergencia e integrando me queda imposible de largo.
Gracias
Buenas, estoy trancado en este ejercicio (Feb2015 ej 4), planteando la divergencia e integrando me queda imposible de largo.
Gracias

A partir del teorema de Gauss, se tiene que
siendo  la superficie orientable que limita al sólido
la superficie orientable que limita al sólido 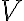 .
.
Siendo
Para la superficie 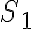 , se tiene que la normal es constante para todos los puntos de
, se tiene que la normal es constante para todos los puntos de 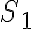 y vale
y vale 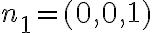 .
.
Haciendo cambio de variable a coordenadas polares cilíndricas, se tiene que  , por lo que se integra
, por lo que se integra  entre
entre  y
y 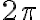 , y
, y 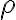 entre
entre  y
y 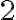 , con
, con 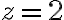 .
.
Para la superficie 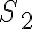 , se tiene que la normal es constante para todos los puntos de
, se tiene que la normal es constante para todos los puntos de 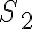 y vale
y vale  .
.
Haciendo cambio de variable a coordenadas polares cilíndricas, se tiene que 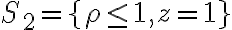 , por lo que se integra
, por lo que se integra  entre
entre  y
y 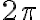 , y
, y 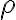 entre
entre  y
y  , con
, con  .
.
Para la superficie 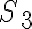 , se tiene que la normal ya no es constante para todos los puntos de
, se tiene que la normal ya no es constante para todos los puntos de 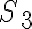 , y vale
, y vale  .
.
Haciendo cambio de variable a coordenadas polares cilíndricas, se tiene que  , por lo que se integra
, por lo que se integra  entre
entre  y
y 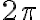 , y
, y 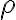 entre
entre  y
y 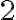 , con
, con 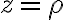 .
.
