Hola, alguien tiene un corolario de ese teorema? ya que en la solución de un ejercicio lo citan y no lo pude encontrar en el libro ni en otros lados, gracias!
En respuesta a Richard Fabian Busca Sellanes
Re: Corolario de Teorema de Dilworth.
En qué ejercicio? Con un poco más de contexto capaz lo identificamos.
En respuesta a Christian Javier Tejeda Farias
Re: Corolario de Teorema de Dilworth.
Practico 8 ejercicio 13:
Muestre que en un conjunto con 61 personas, o bien hay una sucesión de 13 personas cada una de las cuales desciende de la siguiente, o bien hay un grupo de 6 personas ninguna de las cuales es descendiente de alguna otra.
Esa es la letra, yo creo entender que dice que o hay una cadena de 13 elementos o hay una anticadena de 6, como que no pueden pasar ambas y en la solución dice que es por el corolario del teorema de Dilworth.
En respuesta a Richard Fabian Busca Sellanes
Re: Corolario de Teorema de Dilworth.
Según busqué, el corolario (que no recuerdo haber visto en clase, pero no importa) dice así:
Sí 
es un conjunto parcialmente ordenado con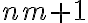 
elementos, entonces existe una cadena de 
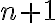elementos y una anticadena de 
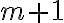elementos.
Para este caso: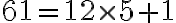 
. Entonces podemos asegurar que existe una cadena de 
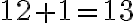y una anticadena de 
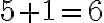elementos.
En respuesta a Christian Javier Tejeda Farias
Re: Corolario de Teorema de Dilworth.
el valor de n y de m los puedo elegir yo o hay alguna regla para ellos?