Octave está pensado para realizar operaciones con vectores y matrices. Tengan esto en cuenta al momento de implementar su código y, siempre que sea posible, traten de expresar sus operaciones en forma vectorial o matricial.
Por ejemplo, supongan que tienen que hacer la suma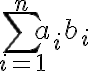 
. Una forma de implementarlo es:
suma = 0;
for i=1:n
suma = suma + a(i)*b(i);
end
Asumiendo que a y b son vectores columna, esto mismo se puede escribir en forma vectorial como:
suma = a'*b;
Esta segunda forma llevará menor tiempo de ejecución. Un algoritmo donde es necesario implementar una suma y pueden usar esta optimización es en Jacobi.
También pueden hacer una mejora de este tipo en EG. Cuando tienen que actualizar la fila i, restándole m veces la fila k, una opción es:
for j=(k+1):n
A(i,j) = A(i,j) - m*A(k,j);
end
Lo anterior se puede escribir en forma vectorial como:
A(i,(k+1):n) = A(i,(k+1):n) - m*A(k,(k+1):n);
Pueden leer más sobre la vectorizacion en:
- https://www.gnu.org/software/octave/doc/v4.0.0/Vectorization-and-Faster-Code-Execution.html
- https://www.mathworks.com/help/matlab/matlab_prog/vectorization.html
Otra forma en que se puede disminuir el tiempo de ejecución es declarando al inicio el tamaño de los arreglos que utilicen, en lugar de ir aumentando su tamaño dentro de un bucle. Esto se llama "preallocation" y pueden ver un ejemplo en https://www.mathworks.com/help/matlab/matlab_prog/preallocating-arrays.html.