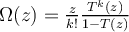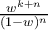Hola Mauri:
Disculpa la demora en responder. He estado complicado, pero ahora te contesto.
Si tú marcas los nodos con k hijos, entonces la generalización de la especificación del ejercicio te da:
T(z,u) = z*(exp(T(z,u)) + (u-1)*T(z,u)^k/k!).
Si aplicas Lagrange es de la forma F = z*Phi(F) donde Phi(v) = exp(v)-(u-1)*v^k/k!.
Entonces [z^n] T(z,u) = 1/n*[v^(n-1)] (Phi(v) = exp(v)-(u-1)*v^k/k!)^n.
Haciendo la expansión de Newton te queda 1/n*[v^(n-1)] sum(binomial(n,j)*exp((n-j)*v)*(u-1)^j*(v^k/k!)^j,j=0..n).
Extraer coeficientes es fácil, pero es aún más fácil! Para la acumulativa tenés que derivar en u, y evaluar en u=1. Entonces todas las potencias (u.1)^j luego de la derivación van a quedar 0 al evaluar en u=1. Para j=0, la derrivada en u vale 0 porque es una constante. Entonces el único índice que te va a quedar luego de derivar en u y evaluar en 1 es el de j=1 (que al derivar (u-1)*A te queda A).
Entonces la acumulativa te queda 1/n*[v^(n-1)] binomial(n,1)*exp((n-1)*v)*(v^k/k!).
Si extraes los coeficientes te queda (n-1)^(n-1-k)*falling(n,k+1)/(n!*k!)
donde falling(n,k+1) = n*(n-1)*(n-2)*...*(n-k).
Si luego dividis (n-1)^(n-1-k)*falling(n,k+1)/k! por n^(n-1) que es el total, y hacés límite cuando k es fijo y n tiende a infinito te da el n*exp(-1)/k!. Este es el coeficiente de una Poisson de parámetro 1.
Avisame si tenés alguna otra duda.
Tuba.