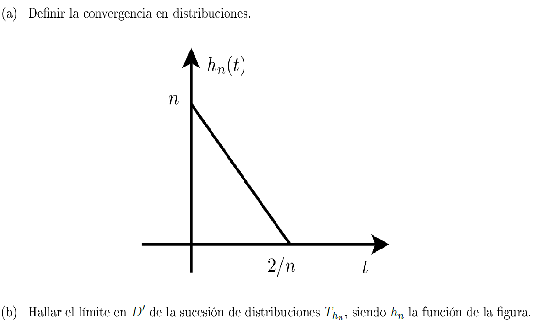
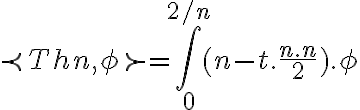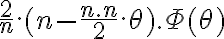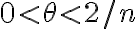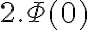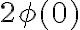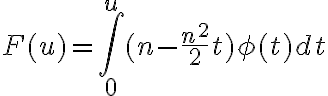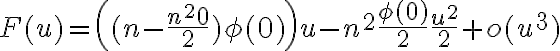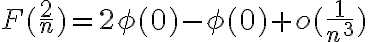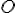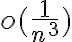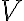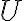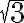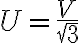Hola que tal? Paso a responderte, primero la convergencia de las distribuciones. Para comenzar observa que el limite que planteaste no da 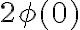 de hecho queda indeterminado, ya que queda 0 por infinito ( el 0 lo aporta
de hecho queda indeterminado, ya que queda 0 por infinito ( el 0 lo aporta  ).
).
Entonces lo que se puede hacer es lo siguiente; consideramos 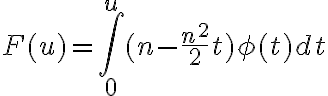 , acá n es fijo dado. Por Taylor hasta el orden 2 y centrado en 0 tenemos que
, acá n es fijo dado. Por Taylor hasta el orden 2 y centrado en 0 tenemos que
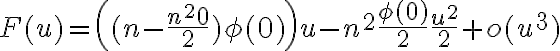
luego
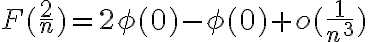 , y como este razonamiento vale para todo n, tomando limite llegamos al resultado deseado, recordando que el termino
, y como este razonamiento vale para todo n, tomando limite llegamos al resultado deseado, recordando que el termino  es un infinitésimo en 0 y por lo tanto tomando n a infinito
es un infinitésimo en 0 y por lo tanto tomando n a infinito 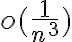 nos tiende a cero .
nos tiende a cero .
Nota: Me parece que formalmente habría que considerar una función de dos variables y Taylor en dos variables pero esta explicación te la toman como correcta
Respecto a lo de trifásica, de polígono a una estrella, la transfiguración busca un sistema de fuentes equivalente en el sentido de que tengamos las mismas tensiones de línea, ya que si esto sucede el resto del circuito "no se entera". Partiendo de nuestro sistema en polígono, las tensiones de líneas son las tensiones de las fuentes de modulo 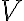 , entonces necesitamos tres fuentes en estrella tal que el modulo de las tensiones en las líneas sea precisamente
, entonces necesitamos tres fuentes en estrella tal que el modulo de las tensiones en las líneas sea precisamente 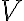 , para eso como las tensiones de líneas son "la resta de los voltajes
, para eso como las tensiones de líneas son "la resta de los voltajes 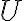 de las fuentes" y sabiendo que la resta de un modulo
de las fuentes" y sabiendo que la resta de un modulo 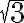 veces más grande tenemos que
veces más grande tenemos que 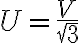 . En realidad necesitamos hacer esto con los angulos también, los sistemas de fuentes defiriran en 30 grados, si es más o menos depende de como conectaste las fuentes, por lo que a la hora de transfigurar te recomiendo comenzar conectado las fuentes en estrellas, ponerles un número a cada una y mediante un diagrama fasorial observar los defasajes. Básicamente es eso. Disculpa si fue escueto, espero haber sido de ayuda.
. En realidad necesitamos hacer esto con los angulos también, los sistemas de fuentes defiriran en 30 grados, si es más o menos depende de como conectaste las fuentes, por lo que a la hora de transfigurar te recomiendo comenzar conectado las fuentes en estrellas, ponerles un número a cada una y mediante un diagrama fasorial observar los defasajes. Básicamente es eso. Disculpa si fue escueto, espero haber sido de ayuda.
Saludos,
Alejandro