Lo que yo hice fue usar Gauss e integrar con respecto al borde del volumen que me queda. Pero cuando parametrizo y hago la integral me da cero. Algo estoy haciendo mal y no me doy cuenta.
En respuesta a Tamara Camila Martinez Santos
Re: Examen Febrero 2015 Ejercicio 4
No lo hice, pero supongo que cuando calculas el flujo de la superficie te falta algo, en este caso creo que es un cono con dos tapas, entonces la superficie total es la union de las 2 tapas más el cono truncado, en este caso serian 3 parametrizaciones para calcular el flujo, luego el flujo es la suma de las 3, capaz que te olvidastes de alguna.
En respuesta a Daniel Nicolas Cardozo Ponciolo
Re: Examen Febrero 2015 Ejercicio 4
Entiendo, la cosa es que el volumen esta delimitado por x^2 + y^2 <= z^2 y 1<= z <=2, entonces el volumen restante no es un cono y no se como parametrizar lo que me queda.
En respuesta a Tamara Camila Martinez Santos
Re: Examen Febrero 2015 Ejercicio 4
Es un cono truncado, lo podes parametrizar asi, como la union de 3 superficies:
la primera es la interseccion de x^2 + y^2 <= z^2 y el plano z=2 que te da un disco
la segunda lo mismo pero con z=1, es otro disco
para lo que te queda entre ambos hay una sugerencia de usar coordenadas cilíndricas, podes pensarlo primero como un cilindro con las dos tapas y luego ves la expresión del ro
Ps: igual capaz que esta mal lo que dije, despues lo voy a hacer y lo verifico
En respuesta a Daniel Nicolas Cardozo Ponciolo
Re: Examen Febrero 2015 Ejercicio 4
Te salio alfinal?, yo intente hacerlo y llegue a que el flujo en ambas tapas es 0 y se me complico para poder parametrizar la superficie entre ambas, en las diapositivas de jana esta la parametrización del cono pero no me doy cuenta como ajustar los parametros para que quede como en este caso, alternativamente esta la opción de calcular la integral triple de la divergencia hay si con cilindricas pero me parece bastante largo y no creo que sea la idea, estaria bueno que algun docente pudiera aportar alguna solución mas accesible.
En respuesta a Daniel Nicolas Cardozo Ponciolo
Re: Examen Febrero 2015 Ejercicio 4
de Micaela Rojas Varela -
Yo tambien tengo la misma duda, lo hice de las dos formas y usando Gauss queda una integral bastante larga que no termine de resolver, con el otro método el flujo en las tapas me quedo cero
En respuesta a Micaela Rojas Varela
Re: Examen Febrero 2015 Ejercicio 4
Mira, yo la parametrizacion que trate de usar para la superficie fue phi(u,v)=(vcos(u),vsin(u),v) y el dominio era [0,2pi]x[1,2], osea trate de modificar la expresion generica de la parametrizacion del cono, calcule el flujo con eso y me dio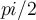 
y la solucion es 
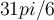, suponiendo que la solucion esta bien entonces la parametrizacion estaria mal, pero no la estaria sacando..
En respuesta a Daniel Nicolas Cardozo Ponciolo
Re: Examen Febrero 2015 Ejercicio 4
Yo al final no lo pude hacer. Lo deje por ahi, intente de la manera que habias dicho y no me quedo.
En respuesta a Daniel Nicolas Cardozo Ponciolo
Re: Examen Febrero 2015 Ejercicio 4
de Gustavo Guerberoff -
Hola, hay que usar Gauss: la superficie es un cono truncado y en las tapas el flujo de F es 0 pues la tercera componente del campo se anula allí (y las normales son (0,0,1) y (0,0,-1)). Para la parametrización de la superficie lateral es correcta la expresión que escribe Daniel arriba: "phi(u,v)=(vcos(u),vsin(u),v) y el dominio [0,2pi]x[1,2]"
Si calculan con esa parametrización los vectores normales, verán que el flujo sobre la superficie lateral queda la integral doble de [v^2 - v(v-2)(v-1)], con v entre 1 y 2, y u entre 0 y 2pi. Las cuentas son un poco tediosas pero el resultado final es la respuesta que se indica.
Recomiendo fuertemente que hagan las cuentas. Saludos, Gustavo.
Lo hice de esa manera y llegue al resultado. En este ejercicio que no dice para donde va la normal, la asumis hacia afuera? y si es asi, no te quedaría un menos?
Exacto. En el teorema de Gauss la normal es saliente. Y en este caso la normal calculada con esa parametrización es saliente porque la tercera componente de n es negativa.
En respuesta a Gustavo Guerberoff
Re: Examen Febrero 2015 Ejercicio 4
Salio alfinal, era un tema de cuentas.