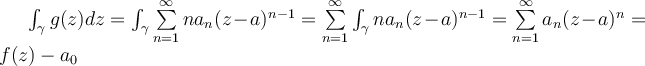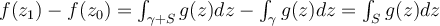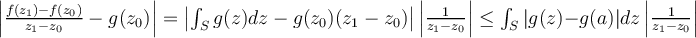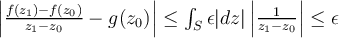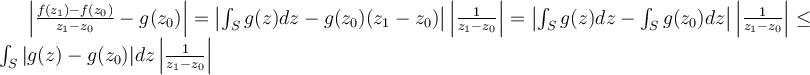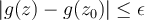Anduve buscando usar los resultados de convergencia uniforme para que la prueba de este teorema sea más natural y me gustaría saber si la prueba es correcta.
Teorema:  analítica en
analítica en  entonces
entonces 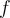 es holomorfa en
es holomorfa en 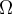 y su derivada es desarrollable.
y su derivada es desarrollable.
Dem:
Dado  y sea
y sea  tal que
tal que 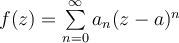 . Claramente el radio de convergencia de la serie es mayor a
. Claramente el radio de convergencia de la serie es mayor a 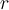 .
.
Consideramos ahora la expresión 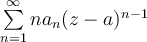 , con el limite superior de la raíz enésima se ve que tiene el mismo radio que la primera serie y por lo tanto tiene sentido definir
, con el limite superior de la raíz enésima se ve que tiene el mismo radio que la primera serie y por lo tanto tiene sentido definir 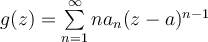 con
con 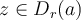 . Probaré que
. Probaré que 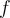 es holomorfa y
es holomorfa y 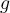 es su derivada. Para eso observo que
es su derivada. Para eso observo que 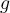 converge uniformemente en cualquier compacto dentro de su radio de convergencia y por lo tanto lo hace para toda curva en el disco. Entonces dado
converge uniformemente en cualquier compacto dentro de su radio de convergencia y por lo tanto lo hace para toda curva en el disco. Entonces dado  y
y 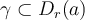 cualquiera que una a con z. Entonces se cumple que
cualquiera que una a con z. Entonces se cumple que
Donde la segunda igualdad vale por convergencia uniforme. La integral de cada termino de la serie en 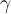 se calcula fácil por conocer las primitivas. Entonces, recordando que
se calcula fácil por conocer las primitivas. Entonces, recordando que 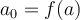 hasta ahora tenemos que
hasta ahora tenemos que
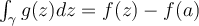
 que una
que una 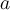 con
con 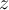 . Probaré ahora que
. Probaré ahora que 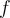 es holomorfa en el disco y su derivada es
es holomorfa en el disco y su derivada es 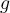 para eso tomo
para eso tomo 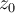 fijo y
fijo y 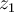 para el primer punto sea una curva cualquiera
para el primer punto sea una curva cualquiera 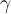 que lo una con
que lo una con 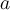 luego para
luego para 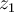 tomo la curva
tomo la curva 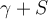 donde S es el segmento de recta que va desde
donde S es el segmento de recta que va desde 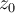 y
y 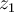 . Entonces
. Entonces
Para continuar, si tomo 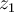 lo suficientemente cerca de
lo suficientemente cerca de 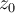 garantizo que
garantizo que  y por lo tanto de la anterior desiguladad
y por lo tanto de la anterior desiguladad  . Por lo tanto
. Por lo tanto 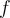 es derivable en el disco, en particular en
es derivable en el disco, en particular en 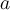 , y como
, y como 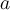 es arbitrario
es arbitrario 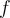 es derivable en
es derivable en 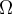 además su derivada es igual a
además su derivada es igual a 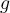 por lo tanto la derivada de
por lo tanto la derivada de 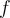 es analítca en
es analítca en 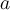 .
.