Alguien me podría indicar que es lo que estoy haciendo mal en este ejercicio? le he dado vueltas para todos lados y no encuentro el error... dejo imagen adjunta
Muchas gracias!
Alguien me podría indicar que es lo que estoy haciendo mal en este ejercicio? le he dado vueltas para todos lados y no encuentro el error... dejo imagen adjunta
Muchas gracias!

Buenas.
En tu primera aplicación del 2.4.5, veo que pusiste 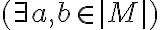 pero deberías haber puesto
pero deberías haber puesto 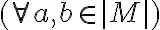 .
.
Me parece que tu error es a partir de la linea en que decis:
Ahí yo usaría la definición de |= y de valuación, y diria que:
Ya que tenes que M modela a 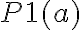 sii M modela a
sii M modela a 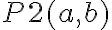 , y por definición de |= :
, y por definición de |= :
Entonces, te quedaría algo así:
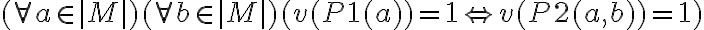 , y esto se tiene que cumplir para toda M del tipo adecuado.
, y esto se tiene que cumplir para toda M del tipo adecuado.
Que en un paso más quedaría:
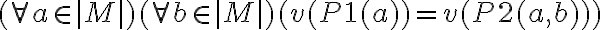 , para que se cumpla el Si y solo si.
, para que se cumpla el Si y solo si.
Como tenes que probar eso para toda estructura M del tipo adecuado, tal que M modela a  (es decir, que M modela a
(es decir, que M modela a  ,
, 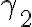 y
y 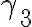 ), y a priori no tenes todas esas estructuras, a mi me resultó más fácil hacer todo suponiendo que M |-
), y a priori no tenes todas esas estructuras, a mi me resultó más fácil hacer todo suponiendo que M |- 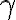 y tratar de llegar al absurdo. (Recordá que por la parte a, sabemos que
y tratar de llegar al absurdo. (Recordá que por la parte a, sabemos que 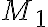 modela
modela 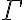 )
)
Perdoná si quedó media confusa la explicación. Espero haberte ayudado, más que confundido.
Saludos.
Gracias Maximiliano!! Pero se me generó otra duda ahora.. según tengo entendido si M "no modela" a algo los "para todo" pasan a ser "existe" por el 2.3.5 (otra lectura) que está en el teórico para cuando algo "no modela", no es así?
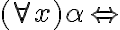
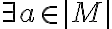 tal que M "no modela" a
tal que M "no modela" a ![\alpha [a/x] \alpha [a/x]](https://eva.fing.edu.uy/filter/tex/pix.php/d9d4f629f55309bf30dd694305925b5e.gif) .
.