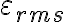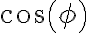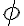[1] P=femrms.Irms.cos(ø)
[2] femrms=femmax/raíz(2)
[3] Irms=femrms/Z
[4] Z=R (en este caso, pues XL=XC)
[5] cos(ø)=R/Z=1
Sustituyo [2], [3], [4] y [5] en [1] y me queda P = femmax2/2R = 2,5 W siendo femmax la amplitud de E1 o E2.
Luego como las 2 fuentes están en serie, la potencia media entregada por ambas es el doble de la calculada, 5 W.
Agradezco comentarios! Saludos